《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

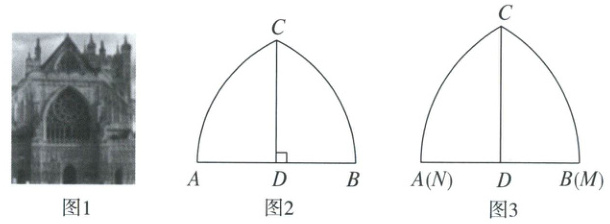
22. (10 分) 在古今中外许多著名建筑中，有很多应用圆弧设计的元素。如图 1，哥特式尖拱是由两段不同圆心的圆弧组成的对称图形，叫做两心尖拱。图 2 是两心尖拱的示意图，其中，点 $A$，$B$ 称为起拱处，点 $C$ 称为拱尖，$C$ 到 $AB$ 的距离 $CD$ 称为拱高，$\overset{\frown}{AC}$ 与 $\overset{\frown}{BC}$ 关于直线 $CD$ 成轴对称，$\overset{\frown}{AC}$ 和 $\overset{\frown}{BC}$ 的圆心分别是点 $M$，$N$，且 $M$，$N$ 恰好落在直线 $AB$ 上。
（1）如图 3，当点 $M$ 恰好与 $B$ 重合，点 $N$ 恰好与 $A$ 重合，若 $CD = 9\ m$，求 $\overset{\frown}{AC}$ 所在圆的半径长；
（2）若图 2 中，$CD = 10\ m$，$AB = 12\ m$，求两心尖拱的两个圆心 $M$，$N$ 之间的距离。

答案：
22.解：
(1)连结MC，如图1。

设$MC = MA = Rm$，由题可知$AD = MD = \frac{1}{2}AB = \frac{1}{2}R$，在$Rt\triangle MCD$中，$MD^2 + CD^2 = MC^2$，$\therefore \frac{1}{4}R^2 + 81 = R^2$，解得$R = 6\sqrt{3}$，故$\overset{\frown}{AC}$所在圆的半径长为$6\sqrt{3}m$。
(2)如图2，在图中作出圆心M、圆心N，过M作$MH\perp AC$于点H。

$\because CD = 10m$，$AB = 12m$，$\therefore AD = BD = \frac{1}{2}AB = 6m$，在$Rt\triangle ADC$中，$AC = \sqrt{AD^2 + CD^2} = 2\sqrt{34}$。由垂径定理可知MH垂直平分AC，$\therefore AH = CH = \frac{1}{2}AC = \sqrt{34}$。$\because \angle CAD = \angle HAM$，$\angle AHM = \angle ADC = 90°$，$\therefore \triangle CAD\sim \triangle MAH$，$\therefore \frac{AC}{AM} = \frac{AD}{AH}$，$\therefore \frac{2\sqrt{34}}{AM} = \frac{6}{\sqrt{34}}$，解得$AM = \frac{34}{3} ＜ AB$，$\therefore$点M和点N在线段AB上。$\because AC$与BC关于直线CD成轴对称，$\therefore AM = BN$。$\because AM + BN - MN = AB$，即$\frac{34}{3} + \frac{34}{3} - MN = 12$，$\therefore MN = \frac{32}{3}m$，故两心尖拱的两个圆心M，N之间的距离为$\frac{32}{3}m$。

23. (10 分) 设二次函数 $y = ax^2 + bx + 1(a \neq 0,a,b$ 是常数），已知函数值 $y$ 和自变量 $x$ 的部分对应取值如表所示：

（1）若 $p = 4$，求二次函数的表达式；
（2）当 $-1 \leq x \leq 4$ 时，$y$ 有最小值为 $-1$，求 $a$ 的值；
（3）求 $2p - q^2$ 的最大值。

答案： 23.解：
(1)$\because$图象过$(0,1)$，$(2,1)$，$\therefore$对称轴是直线$x = \frac{0 + 2}{2} = 1$，$\therefore -\frac{b}{2a} = 1$，$\therefore b = -2a$，$\therefore$二次函数为$y = ax^2 + bx + 1 = ax^2 - 2ax + 1$。又图象过$(-1,4)$，$\therefore 4 = a + 2a + 1$，$\therefore a = 1$，$\therefore$二次函数的表达式为$y = x^2 - 2x + 1$。
(2)由题意，抛物线的对称轴是直线$x = 1 = -\frac{b}{2a}$，$\therefore b = -2a$。
①当$a ＞ 0$时，$\because -1\leqslant x\leqslant4$，$\therefore$当$x = 1$时，y取最小值为$a + b + 1 = a - 2a + 1 = -1$，$\therefore a = 2$。
②当$a ＜ 0$时，$\because$抛物线上的点离对称轴越远函数值越小，$-1\leqslant x\leqslant4$，$\therefore$当$x = 4$时，y取最小值为$16a + 4b + 1 = 16a - 8a + 1 = -1$，$\therefore a = -\frac{1}{4}$。
综上，$a = 2$或$a = -\frac{1}{4}$。
(3)抛物线的对称轴是直线$x = -\frac{b}{2a} = 1$，$\therefore b = -2a$。又$\because p = a - b + 1$，$q = a + b + 1$，$\therefore p = 3a + 1$，$q = -a + 1$。$\therefore 2p - q^2 = 2(3a + 1) - (-a + 1)^2 = 6a + 2 - a^2 + 2a - 1 = -a^2 + 8a + 1 = -(a - 4)^2 + 17$。$\therefore$当$a = 4$时，$2p - q^2$的最大值为17。