《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

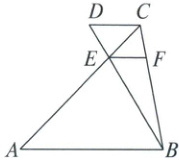
21. (7 分)如图,$AB// CD$,AC,BD 交于点 E,过点 E 作$EF// AB$交 BC 于点 F.已知$AE = BC$,$CE = 3$.设$CF = x$,$AE = y$.
(1)求 y 关于 x 的函数解析式;
(2)若$CF = 2$,$AB = 8$,求 CD 的长.

答案： 21.解：
(1)$\because EF// AB$交BC于点F，$AE = BC$，$CE = 3$，$CF = x$，$AE = y$，$\therefore \frac{CE}{CA}=\frac{CF}{CB}$，
$\therefore \frac{3}{3 + y}=\frac{x}{y}$，$\therefore y=\frac{3x}{3 - x}$.
(2)当$x = CF = 2$时，$y = AE=\frac{3x}{3 - x}=6$，
$\because AB// CD$，$\therefore \triangle ABE\backsim \triangle CDE$，$\therefore \frac{CD}{AB}=\frac{CE}{AE}$，
$\because AB = 8$，$\therefore \frac{CD}{8}=\frac{3}{6}$，$\therefore CD = 4$.

22. (8 分)【项目】小车沿斜面运动中路程 s 与时间 t 的关系.
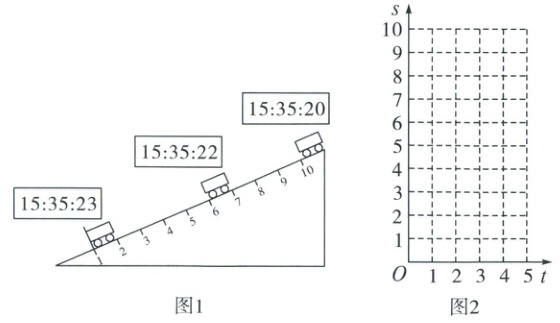
图 1 是小车从斜面上静止滑下的实验装置,斜面刻度值单位为分米.小温和小州共同填写了如下实验记录表:

(1)小温发现,路程 s 与时间 t 可采用一次函数、反比例函数、二次函数中的一种进行刻画,请通过实验数据在图 2 中描点画图,判断可以采用的函数模型,并求出 s 关于 t 的函数解析式;
(2)若斜面足够长,请通过计算说明小车在斜面上第 1 个 5 秒和第 2 个 5 秒通过的路程之差;
(3)小州说:“把单位时间设为 1 秒,还可以研究第 t 秒内通过的路程$s'$(分米)与第 t 秒之间的函数关系.”
请写出一个路程$s'$(分米)与第 t 秒之间的结论,并通过计算说明理由.

答案：
22.解：
(1)将题中给出的实验数据在图中描点，依次连结各点，如图所示.

可以采用的函数模型是二次函数，
设路程s与时间t的函数关系式为$s = at^{2}+bt + c(a\neq0)$，
将$(0,0),(2,4),(3,9)$代入，得$\begin{cases}c = 0\\4a + 2b + c = 4\\9a + 3b + c = 9\end{cases}$，解得$\begin{cases}a = 1\\b = 0\\c = 0\end{cases}$
$\therefore s$关于t的函数解析式为$s = t^{2}(t\geqslant0)$.
(2)当$t = 5$时，$s = 5^{2}=25$分米，当$t = 10$时，$s = 10^{2}=100$分米，
$\therefore$第2个5秒小车通过的路程为$100 - 25 = 75$分米，
$\therefore$路程差为$75 - 25 = 50$分米.
(3)第1秒通过的路程$=1^{2}=1$分米，第2秒通过的路程$=2^{2}-1^{2}=3$分米，第3秒通过的路程$=3^{2}-2^{2}=5$分米，$·s·s$，第t秒通过的路程$=t^{2}-(t - 1)^{2}=(2t - 1)$分米，
$\therefore$第t秒内通过的路程$s^{\prime}$（分米）与第t秒之间的函数关系为$s^{\prime}=2t - 1$.