第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
21. (8分)糖炒板栗是深受大家喜爱的小吃。已知糖炒板栗每斤(斤:我国市制质量单位)成本大约为10元。某店家试销阶段每斤的销售价$x$(元)与糖炒板栗日销售量$y$(斤)之间的关系如表:

若日销售量$y$是销售价$x$的一次函数,试求:
(1)日销售量$y$(斤)与销售价$x$(元)的函数关系式;
(2)假设后续销售情况与试销阶段效果相同,要使这种糖炒板栗每日销售的利润$w$最大,每斤的销售价应定为多少元?每日销售的最大利润是多少元?

若日销售量$y$是销售价$x$的一次函数,试求:
(1)日销售量$y$(斤)与销售价$x$(元)的函数关系式;
(2)假设后续销售情况与试销阶段效果相同,要使这种糖炒板栗每日销售的利润$w$最大,每斤的销售价应定为多少元?每日销售的最大利润是多少元?
答案:
21.解:
(1)设$y = kx + b$,把$(15,100)$,$(20,80)$代入$y = kx + b$中,得$\begin{cases}100 = 15k + b\\80 = 20k + b\end{cases}$,解得$\begin{cases}k = -4\\b = 160\end{cases}$,$\therefore y = -4x + 160$.
(2)由题意,得$w = y(x - 10)=(-4x + 160)(x - 10)=-4x^2 + 200x - 1600=-4(x - 25)^2 + 900$,$\because a = -4 < 0$,$\therefore$当$x = 25$时,$w_{最大}=900$元,$\therefore$每斤的销售价应定为$25$元,每日销售的最大利润是$900$元.
(1)设$y = kx + b$,把$(15,100)$,$(20,80)$代入$y = kx + b$中,得$\begin{cases}100 = 15k + b\\80 = 20k + b\end{cases}$,解得$\begin{cases}k = -4\\b = 160\end{cases}$,$\therefore y = -4x + 160$.
(2)由题意,得$w = y(x - 10)=(-4x + 160)(x - 10)=-4x^2 + 200x - 1600=-4(x - 25)^2 + 900$,$\because a = -4 < 0$,$\therefore$当$x = 25$时,$w_{最大}=900$元,$\therefore$每斤的销售价应定为$25$元,每日销售的最大利润是$900$元.
22. (10分)司南是我国古代辨别方向用的一种仪器,早在战国时期就已被发明,是现代所用指南针的始祖(如图1)。司南中心为一圆形,圆心为点$O$,直径为20cm,根据八个方位将圆形八等分(图2中的点$A \sim H$),连结$DG$,$BH$并延长交于点$P$。
(1)点$P$位于点$D$的北偏东
(2)求$PH$的长;
(3)连结$BG$,比较线段$BG$与$PH$大小。(写出你作出判断的理由)
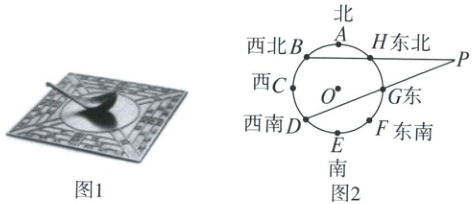
(1)点$P$位于点$D$的北偏东
67.5°
的方向上;(2)求$PH$的长;
(3)连结$BG$,比较线段$BG$与$PH$大小。(写出你作出判断的理由)

答案:
22.解:
(1)如图1,连结$OB$,$OG$,$BD$,

$\because$八个方位将圆形八等分,$\therefore \stackrel\frown{AB}=\stackrel\frown{AH}=\stackrel\frown{GH}=\frac{360°}{8}=45°$,$\therefore \angle BOG = 45° × 3 = 135°$,$\therefore \angle BDP=\frac{1}{2}\angle BOG = 67.5°$,即点$P$位于点$D$的北偏东$67.5°$的方向上,故答案为$67.5°$.
(2)如图2,连结$BD$,$DH$,则$DH$为直径,

$\therefore \angle B = 90°$,$DH = 20 cm$,由
(1)知$\angle BDP = 67.5°$,$\therefore \angle P = 90° - 67.5° = 22.5°$.$\because HG$所对的圆心角为$45°$,$\therefore \angle HDG=\frac{1}{2} × 45° = 22.5°$,$\therefore PH = DH = 20 cm$.
(3)$PH>BG$.理由如下:如图3,连结$OG$,$BF$,过点$G$作$GM \perp BF$交$BF$于点$M$,

$\because \angle GOM = 45°$,$OG = 10 cm$,$\therefore GM = OM = 5\sqrt{2} cm$,$\therefore BM = OB + OM = (10 + 5\sqrt{2}) cm$,在$Rt\triangle BGM$中,$BG^2 = BM^2 + GM^2 = 200 + 100\sqrt{2}<400$,$\because PH^2 = 400$,$\therefore PH^2>BG^2$,故$PH>BG$.
22.解:
(1)如图1,连结$OB$,$OG$,$BD$,

$\because$八个方位将圆形八等分,$\therefore \stackrel\frown{AB}=\stackrel\frown{AH}=\stackrel\frown{GH}=\frac{360°}{8}=45°$,$\therefore \angle BOG = 45° × 3 = 135°$,$\therefore \angle BDP=\frac{1}{2}\angle BOG = 67.5°$,即点$P$位于点$D$的北偏东$67.5°$的方向上,故答案为$67.5°$.
(2)如图2,连结$BD$,$DH$,则$DH$为直径,

$\therefore \angle B = 90°$,$DH = 20 cm$,由
(1)知$\angle BDP = 67.5°$,$\therefore \angle P = 90° - 67.5° = 22.5°$.$\because HG$所对的圆心角为$45°$,$\therefore \angle HDG=\frac{1}{2} × 45° = 22.5°$,$\therefore PH = DH = 20 cm$.
(3)$PH>BG$.理由如下:如图3,连结$OG$,$BF$,过点$G$作$GM \perp BF$交$BF$于点$M$,

$\because \angle GOM = 45°$,$OG = 10 cm$,$\therefore GM = OM = 5\sqrt{2} cm$,$\therefore BM = OB + OM = (10 + 5\sqrt{2}) cm$,在$Rt\triangle BGM$中,$BG^2 = BM^2 + GM^2 = 200 + 100\sqrt{2}<400$,$\because PH^2 = 400$,$\therefore PH^2>BG^2$,故$PH>BG$.
查看更多完整答案,请扫码查看


