《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

1. 若$\frac{a}{b}=\frac{3}{5}$，则$\frac{a + b}{b}$的值是(C)

A.$\frac{5}{8}$
B.$\frac{3}{5}$
C.$\frac{8}{5}$
D.$\frac{3}{2}$

答案： 1.C　解析:
∵$\frac{a}{b}$=$\frac{3}{5}$，
∴可设a=3k，那么b=5k，
∴$\frac{a+b}{b}$=$\frac{3k+5k}{5k}$=$\frac{8}{5}$。
　故选C。

2. 若$\triangle ABC \backsim \triangle DEF$，$\triangle ABC$与$\triangle DEF$的面积比为$1:16$，则$AB$与$DE$的比是(A)

A.$1:4$
B.$1:8$
C.$1:16$
D.$1:32$

答案： 2.A　解析:
∵△ABC∽△DEF，
∴$\frac{S_{\triangle ABC}}{S_{\triangle DEF}}$=($\frac{AB}{DE}$)²=$\frac{1}{16}$，
∴$\frac{AB}{DE}$=$\frac{1}{4}$。
　故选A。

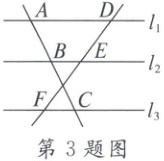
3. 已知$l_1 // l_2 // l_3$，$\frac{AB}{BC}=\frac{3}{5}$，$DE = 9$，则$EF =$(B)

A.$12$
B.$15$
C.$28$
D.$24$

答案： 3.B　解析:
∵$l_1 // l_2 // l_3$，
∴$\frac{AB}{BC}$=$\frac{DE}{EF}$，
∴$\frac{3}{5}$=$\frac{9}{EF}$，
∴EF=15。
　故选B。

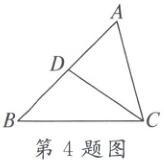
4. 如图，$D$是$\triangle ABC$的边$AB$上的一点，那么下列四个条件不能单独判定$\triangle ABC \backsim \triangle ACD$的是(C)

A.$\angle B = \angle ACD$
B.$\angle ADC = \angle ACB$
C.$\frac{AC}{CD}=\frac{AB}{BC}$
D.$AC^2 = AD · AB$

答案： 4.C　解析:
∵∠A是公共角，
∴再加上∠B=∠ACD，或∠ADC=∠ACB都可判定△ABC∽△ACD。
∵∠A是公共角，再加上$AC^2=AD · AB$，即$\frac{AC}{AD}$=$\frac{AB}{AC}$，也可判定△ABC∽△ACD。
∴选项A、B、D都可判定△ABC∽△ACD。
　　而选项C中的两边成比例，但不是相应的夹角相等，所以选项C不能。
　　故选C。

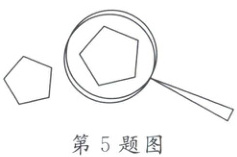
5. 如图，用放大镜看到的多边形与原多边形相比较，不发生改变的是(C)

A.周长
B.面积
C.每个内角的度数
D.每条边的长度

答案： 5.C　解析:由题意得，用放大镜看到的多边形与原多边形是相似的关系，
　　用放大镜看到的多边形与原多边形相比较，周长、面积、每条边的长度均增大了，每个内角的度数保持不变。
　　故选C。

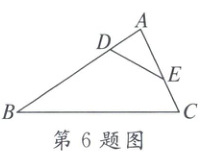
6. 如图，$\triangle AED \backsim \triangle ABC$，$\angle A = 80^{\circ}$，$\angle B = 35^{\circ}$，则$\angle ADE$等于(C)

A.$80^{\circ}$
B.$75^{\circ}$
C.$65^{\circ}$
D.$35^{\circ}$

答案： 6.C　解析:
∵△AED∽△ABC，
∴∠C=∠ADE，
∵∠A=80°，∠B=35°，
∴∠ADE=∠C=180°−80°−35°=65°。
　　故选C。

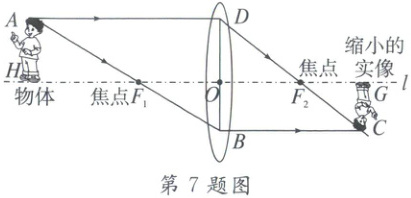
7. 凸透镜成像的原理如图所示，$AD // l // BC$。若物体到焦点$F_1$的距离与焦点$F_1$到凸透镜的中心线$DB$的距离之比为$5:4$，则物体被缩小到原来的(D)

A.$\frac{5}{9}$
B.$\frac{4}{9}$
C.$\frac{3}{4}$
D.$\frac{4}{5}$

答案： 7.D　解析:
∵BC//l，CG⊥l，BO⊥l，
∴四边形OBCG为矩形，
∴OB=CG，
∵AH⊥HO，BO⊥HO，
∴△AHF₁∽△BOF₁，
∴$\frac{AH}{BO}$=$\frac{HF_1}{OF_1}$=$\frac{5}{4}$，
∴$\frac{AH}{CG}$=$\frac{5}{4}$。
∴物体被缩小到原来的$\frac{4}{5}$。

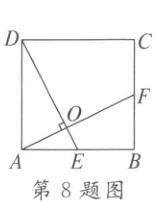
8. 如图，正方形$ABCD$中，$E$为$AB$的中点，$AF \perp DE$于点$O$，则$\frac{AO}{DO}$等于(A)

A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{2}{3}$
D.$\frac{2\sqrt{5}}{3}$

答案： 8.A　解析:
∵四边形ABCD是正方形，
∴AB=AD，∠BAD=90°，
∴∠DAO+∠EAO=90°，
∵E为AB的中点，
∴AE=$\frac{1}{2}$AB=$\frac{1}{2}$AD，
∵AF⊥DE，
∴∠AOE=∠DOA=90°，
∴∠DAO+∠ADO=90°，
∴∠EAO=∠ADO，
∴△AOE∽△DOA，
∴$\frac{AO}{DO}$=$\frac{AE}{AD}$=$\frac{1}{2}$。
　故选A。