《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

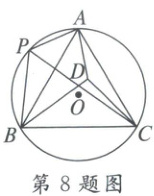
8. 如图，点P是圆O劣弧AB上的一个动点(不与点A，B重合)，且满足∠BPC=∠APC=60°，D是△ABC内一点，AD=3，CD=4，BD=5，点P在劣弧AB上运动的过程中，$2m = PA^{2} + PB^{2} + PC^{2}$，则m的值满足(B)

A.$0 ＜ m ＜ 25 + 12\sqrt{3}$
B.$m = 25 + 12\sqrt{3}$
C.$25 + 12\sqrt{3} ＜ m ＜ 50$
D.$m = 50$

答案：
8.B　解析:如图，延长BP到点F,使得PF=AP,过点A 作AE⊥PF于点E,
　　　　　　　　　
∵∠BPC=∠APC=60°,
∴∠APB=∠BPC+∠APC=120°,
　则∠APF=180°−∠APB=60°,
∵∠APF=60°,PF=AP,
∴△APF是等边三角形，
∴AF=AP、∠FAP=60°。,
∵∠BPC=∠APC=60°,
∴AC=BC,
∵A,B,C,P四点共圆,∠APB=120°,
∴∠ACB=180°−∠APB=60°,
∴△ABC是等边三角形，
∴AB=AC,∠BAC=60°,
∵∠FAP=∠BAC=60°,
∴∠FAP+∠PAB=∠BAC+∠PAB,
　即∠FAB=∠PAC,
∴△FAB≌△PAC(SAS),
∴BF=PC,
　即PC=PF+BP=AP+BP,
∵AE⊥BE,
∴∠PAE=90°−∠APE=30°,
　故$PE=\frac{1}{2}AP$，
　则$AE=\sqrt{AP^{2}-PE^{2}}$
　=$\sqrt{AP^{2}-(\frac{1}{2}AP)^{2}}=\frac{\sqrt{3}}{2}AP$，
　在Rt△AEB中,$AB^{2}=AE^{2}+BE^{2}$，$BE=BP+PE$，
　即$AB^{2}=(\frac{\sqrt{3}}{2}AP)^{2}+(BP+\frac{1}{2}AP)^{2}$，
　整理,得$AB^{2}=AP^{2}+BP^{2}+BP· AP$，
∵$2m=PA^{2}+PB^{2}+PC^{2}=PA^{2}+PB^{2}+(PB+PA)^{2}=2(PB^{2}+PA^{2}+PB· PA)$，
∴$2m=PA^{2}+PB^{2}+PC^{2}=2AB^{2}$，
∴$m=AB^{2}$，
　将△BCD绕点C顺时针旋转60°得到△ACD'，连结
DD',过点C作CG⊥AD交AD延长线于点G，如图，
　　　　　　　　
　则CD'=CD,AD'=BD=5,∠DCD'=60°.
∴△DCD'是等边三角形，
∴DD'=CD=4,∠D'DC=60°,
∵$AD^{2}+D'D^{2}=3^{2}+4^{2}=25$，$D'A^{2}=5^{2}=25$，
∴$AD^{2}+D'D^{2}=D'A^{2}$，
　即△ADD'是直角三角形，
∴∠ADD'=90°,
∴∠ADC=∠ADD'+∠D'DC=90°+60°=150°,
∴∠GDC=180°−∠ADC=30°,
∴$CG=\frac{1}{2}DC=2$，$DG=\sqrt{DC^{2}-CG^{2}}=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$，
∴$AG=AD+DG=3+2\sqrt{3}$，
　则$AC^{2}=AG^{2}+CG^{2}=(3+2\sqrt{3})^{2}+2^{2}=25+12\sqrt{3}$，
∵AC=AB,
∴$m=AC^{2}=25+12\sqrt{3}$
　故选B.

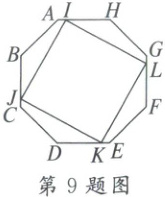
9. 如图，在边长为$\sqrt{2}$的正八边形ABCDEFGH中，已知I，J，K，L分别是边AH，BC，DE，FG上的动点，且满足IA=JC=KE=LG，则四边形IJKL面积的最大值为(A)

A.$4 + 2\sqrt{2}$
B.$2 + 2\sqrt{2}$
C.$4 + \sqrt{2}$
D.$2 + 4\sqrt{2}$

答案：
9.A　解析:如图，连结IK,JL,
　　　　　　　　
∵正八边形ABCDEFGH,IA=JC=KE=LG,
∴IJ=JK=KL=LI,IK=JL,
∴四边形IJKL为正方形，
∴四边形IJKL的面积为$IJ^{2}$，
　当IJ最大时，四边形IJKL的面积最大，
∴IJ=AC，即为正八边形的对角线时，四边形IJKG的面积最大，
　连结AE,CG交于点O，连结OB，交AC于点M，
　则△AOC为等腰直角三角形，O为正八边形的中心，
∴OC=OB=OA,OB垂直平分AC，
∴$OM=AM=\frac{\sqrt{2}}{2}OA$，
　设OM=AM=x,
则OC=OB=OA=$\sqrt{2}x$，
∴$BM=\sqrt{2}x-x$，
　在Rt△AMB中,$AB^{2}=BM^{2}+AM^{2}$，
　即$(\sqrt{2})^{2}=(\sqrt{2}x-x)^{2}+x^{2}$，
　解得$x=\frac{\sqrt{2\sqrt{2}+4}}{2}$(负值不合题意，舍去)，
∴$AC=2AM=\sqrt{2\sqrt{2}+4}$，
∴四边形IJKL的最大面积为$AC^{2}=4+2\sqrt{2}$
　故选A.

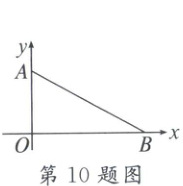
10. 如图，在平面直角坐标系xOy中，点A，B的坐标分别为（0，2）和（4，0），则△OAB的外接圆的圆心坐标是(2,1)。

答案： 10.(2,1)　解析:
∵O,A,B均在圆上,∠AOB=90°,
∴AB是外接圆的直径，
∴外接圆的圆心是AB的中点(2，1).

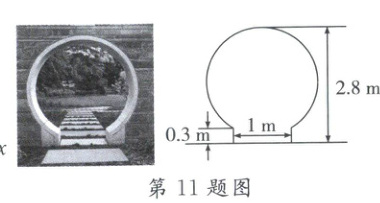
11. 圆在中式建筑中有着广泛的应用。如图，某园林中圆弧形门洞的顶端到地面的高度为2.8m，地面入口的宽度为1m，门枕的高度为0.3m，则该圆弧所在圆的半径为 m。1.3

答案：
11.1.3　解析:设该圆弧所在圆的半径为$r$m，
　　如图，设点O为圆心，过点O作OC⊥AB于点C,延长
CO交圆O于点D，连结OA，
　　　　　　　　
　　则CD=2.8−0.3=2.5m，$AC=BC=\frac{1}{2}AB=\frac{1}{2}×1=0.5(m)$，
∴OC=(2.5−$r$)m，
　　在Rt△AOC中,由勾股定理，得$OA^{2}=AC^{2}+OC^{2}$，
　　即$r^{2}=0.5^{2}+(2.5−r)^{2}$，
　　解得$r$=1.3,
　　即该门洞的半径为1.3m.

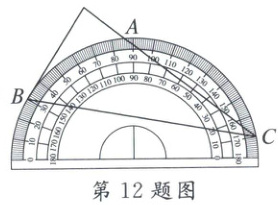
12. 将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上。点A，B的读数分别为86°，30°，则∠ACB的大小为28°。

答案：
12.28°　解析:设半圆圆心为O,连结OA，OB，如图，
∵∠ACB=$\frac{1}{2}$∠AOB,
　　而∠AOB=86°−30°=56°,
∴∠ACB=$\frac{1}{2}$×56°=28°.
　　　　　　

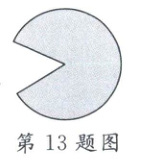
13. 如图，“吃豆小人”是一个经典的游戏形象，它的形状是一个扇形。若扇形弧长为$\frac{5\pi}{3}$，半径为1，则这个“吃豆小人”（阴影图形）的面积为$\frac{5\pi}{6}$。

答案： 13.$\frac{5\pi}{6}$　解析:设扇形的圆心角为$n°$，
∵扇形弧长为$\frac{5\pi}{3}$，半径为1，
∴$\frac{n\pi×1}{180}=\frac{5\pi}{3}$，
∴$n$=300,
∴这个“吃豆小人”(阴影图形)的面积=$\frac{300\pi×1^{2}}{360}=\frac{5\pi}{6}$.

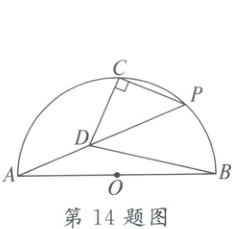
14. 如图，已知以AB为直径的半圆O，C为$\overset{\frown}{AB}$的中点，P为$\overset{\frown}{BC}$上任意一点，CD⊥CP交AP于D，连结BD，若AB=6，则BD的最小值为$3\sqrt{5}-3$。

答案：
14.$3\sqrt{5}-3$　解析:如图，连结AC，以AC为斜边作等腰直角三角形ACQ，则∠AQC=90°，连结BC,BQ,DQ.
　　　　　　　
∵半圆O的直径为AB，C为$\widehat{AB}$的中点，
∴∠APC=45°.
　　又
∵CD⊥CP,
∴∠DCP=90°,
∴∠PDC=45°,∠ADC=135°,
∴点D的运动轨迹为以Q为圆心,AQ为半径的$\widehat{AC}$，
　　又
∵AB=6，C为$\widehat{AB}$的中点，
∴△ACB是等腰直角三角形，
∴$AC=3\sqrt{2}$，
∴在等腰直角△ACQ中,AQ=3,
∴$BQ=\sqrt{3^{2}+6^{2}}=3\sqrt{5}$，
∴$BD\geq BQ-DQ$，
∴BD的最小值为$3\sqrt{5}-3$.

15. 如图1是一款轴对称“磁悬浮地漏”无水时的示意图，它由一个圆弧形密封盖$\overset{\frown}{MN}$与两个磁体组成（下侧磁体固定不动），连结杆EF与地面BD（或AC）垂直，排水口CD=24$\sqrt{3}$cm，密封盖最高点E到地面的距离为6mm，整个地漏的高度EG=75mm（G为磁体底部中点），密封盖被磁体顶起将排水口密封。
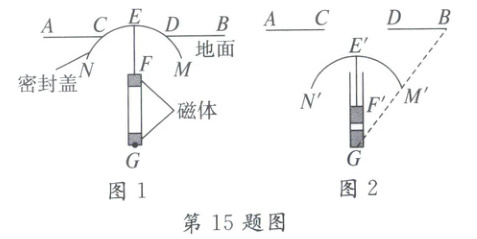
（1）$\overset{\frown}{MN}$所在圆的半径为39mm；
（2）当有水时如图2所示，密封盖下移排水，当密封盖下沉至最低处时，点M恰好落在BG中点M'处，若点M'到E'F'的距离为36mm，则密封盖下沉的最大距离为16.5mm。

答案：
15.
(1)39　
(2)16.5　解析:
(1)如图1,设圆心为O,连结
CD交EF于点H，连接OD，
　设OH=$x$mm,
∵最高点E到地面的距离为6mm,
∴OE=(6+$x$)mm,
∵CD=$24\sqrt{3}$mm,
∴DH=$12\sqrt{3}$mm,
∴在Rt△OHD中，
$OD=\sqrt{x^{2}+(12\sqrt{3})^{2}}$
∵OE=OD,
∴$6+x=\sqrt{x^{2}+(12\sqrt{3})^{2}}$
∴$x$=33,
∴OE=39mm.
∴MN所在圆的半径为39mm.
　　　　　　　　
(2)如图2,连结CD,作M'P'⊥E'G,延长GE'交AB于点Q',作M'Z⊥BD交BD于点Z，
∴M'Z//E'G.
∵M'为BG的中点，
∴M'Z为△GQ'B的中位线，
∴$M'Z=\frac{1}{2}GQ'$.
　由题意知GQ'=75−6=69mm,
∴$M'Z=\frac{1}{2}×69=34.5$mm.
　如图1,作MJ⊥EG,连结OM,
∵点M'到E'F'的距离为36mm,
∴MJ=M'P'=36mm,
　由勾股定理，得$OJ=\sqrt{OM^{2}-MJ^{2}}=\sqrt{39^{2}-36^{2}}=15(mm)$，
∴移动前M到地面的距离为JH=39−15−6=
　18(mm),
∵M移动的距离为密封盖下沉的距离，
　M'Z−JH=34.5−18=16.5(mm),
∴密封盖下沉的最大距离为16.5mm.