第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
9. 图 1 是捣谷物的“碓”,图 2 是其示意图,O 为转动支点,$CD\perp AB$于点 B,AB 与水平线 MN 夹角$\angle BOM = 30^{\circ}$,$BC = 40\ cm$,$OB = 120\ cm$,$OA = 40\ cm$.当点 C 绕点 O 旋转下落到 MN 上时,点 A 上升(
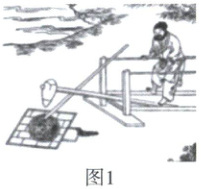
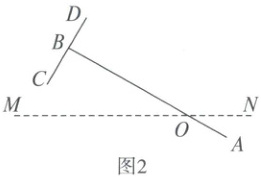
A.$2\sqrt{10}\ cm$
B.$(20 - 2\sqrt{10})\ cm$
C.$4\sqrt{10}\ cm$
D.$(20 - 4\sqrt{10})\ cm$
D
)

A.$2\sqrt{10}\ cm$
B.$(20 - 2\sqrt{10})\ cm$
C.$4\sqrt{10}\ cm$
D.$(20 - 4\sqrt{10})\ cm$
答案:
9.D 解析:将$\triangle OBC$和$OA$绕点O旋转到$\triangle OB^{\prime}C^{\prime}$和$OA^{\prime}$,使点C的对应点为$C^{\prime}$落在$OM$上,
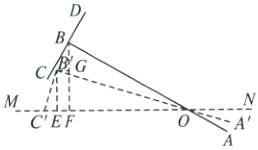
设点A上升的高度为h,过点B作$BF\perp MN$于点F,过$B^{\prime}$作$B^{\prime}E\perp MN$于点E,$B^{\prime}G\perp BF$于点G,
则四边形$B^{\prime}EFG$是矩形,$\therefore FG = B^{\prime}E$,
$\because \angle BOM = 30^{\circ},OB = 120$cm,
$\therefore BF = \frac{1}{2}OB = 60$cm.
$\because CD\perp AB$于点B,$BC = 40$cm,
$\therefore OC = \sqrt{OB^{2}+BC^{2}} = 40\sqrt{10}$cm,
$\therefore OC^{\prime} = 40\sqrt{10}$cm.
$\because \angle OB^{\prime}C^{\prime} = \angle OBC = 90^{\circ}$,
$\therefore \angle OB^{\prime}C^{\prime} = \angle OEB^{\prime} = 90^{\circ}$.
$\because \angle B^{\prime}OC^{\prime} = \angle EOB^{\prime}$,$\therefore \triangle OEB^{\prime}\backsim \triangle OB^{\prime}C^{\prime}$.
$\therefore \frac{B^{\prime}E}{B^{\prime}C^{\prime}}=\frac{OB^{\prime}}{OC^{\prime}}$,
$\because B^{\prime}C^{\prime} = BC = 40$cm,$OB^{\prime} = OB = 120$cm,
$\therefore \frac{B^{\prime}E}{40}=\frac{120}{40\sqrt{10}}$
$\therefore B^{\prime}E = 12\sqrt{10}$cm,$\therefore FG = 12\sqrt{10}$cm,
$\therefore BG = BF - FG=(60 - 12\sqrt{10})$cm,
$\because \frac{h}{BG}=\frac{OA}{OB}$,$OA = 40$cm,
$\therefore h=(20 - 4\sqrt{10})$cm.
故选:D.
9.D 解析:将$\triangle OBC$和$OA$绕点O旋转到$\triangle OB^{\prime}C^{\prime}$和$OA^{\prime}$,使点C的对应点为$C^{\prime}$落在$OM$上,

设点A上升的高度为h,过点B作$BF\perp MN$于点F,过$B^{\prime}$作$B^{\prime}E\perp MN$于点E,$B^{\prime}G\perp BF$于点G,
则四边形$B^{\prime}EFG$是矩形,$\therefore FG = B^{\prime}E$,
$\because \angle BOM = 30^{\circ},OB = 120$cm,
$\therefore BF = \frac{1}{2}OB = 60$cm.
$\because CD\perp AB$于点B,$BC = 40$cm,
$\therefore OC = \sqrt{OB^{2}+BC^{2}} = 40\sqrt{10}$cm,
$\therefore OC^{\prime} = 40\sqrt{10}$cm.
$\because \angle OB^{\prime}C^{\prime} = \angle OBC = 90^{\circ}$,
$\therefore \angle OB^{\prime}C^{\prime} = \angle OEB^{\prime} = 90^{\circ}$.
$\because \angle B^{\prime}OC^{\prime} = \angle EOB^{\prime}$,$\therefore \triangle OEB^{\prime}\backsim \triangle OB^{\prime}C^{\prime}$.
$\therefore \frac{B^{\prime}E}{B^{\prime}C^{\prime}}=\frac{OB^{\prime}}{OC^{\prime}}$,
$\because B^{\prime}C^{\prime} = BC = 40$cm,$OB^{\prime} = OB = 120$cm,
$\therefore \frac{B^{\prime}E}{40}=\frac{120}{40\sqrt{10}}$
$\therefore B^{\prime}E = 12\sqrt{10}$cm,$\therefore FG = 12\sqrt{10}$cm,
$\therefore BG = BF - FG=(60 - 12\sqrt{10})$cm,
$\because \frac{h}{BG}=\frac{OA}{OB}$,$OA = 40$cm,
$\therefore h=(20 - 4\sqrt{10})$cm.
故选:D.
10. 已知二次函数$y = - 3x^{2}+9$.当$-2\leqslant x\leqslant n$时,函数的最大值与最小值的差为 12,则 n 的取值范围是(
A.$-\sqrt{3}\leqslant n\leqslant 0$
B.$0\leqslant n\leqslant 2$
C.$-\sqrt{3}\leqslant n\leqslant 2$
D.$\sqrt{3}\leqslant n\leqslant \sqrt{7}$
B
)A.$-\sqrt{3}\leqslant n\leqslant 0$
B.$0\leqslant n\leqslant 2$
C.$-\sqrt{3}\leqslant n\leqslant 2$
D.$\sqrt{3}\leqslant n\leqslant \sqrt{7}$
答案:
10.B 解析:由条件可知,抛物线在对称轴左侧,y的值随着x的增大而增大;在对称轴右侧,y的值随着x的增大而减小.
①当$n < 0$时,当$-2\leqslant x\leqslant n$时,y随x的增大而增大,那么$x = - 2$时取得最小值,$x = n$时取得最大值,最小值为$-3$,最大值为$-3n^{2}+9$,则可列出方程:$-3n^{2}+9 + 3 = 12$,解得$n = 0$,但是这与假设矛盾,所以这种情况不符合题意,舍去;
②当$0\leqslant n\leqslant2$时,此时$x = 0$时取得最大值,$x = - 2$时取得最小值,最大值为9,最小值为$-3$,此时最大值与最小值的差为12,符合题意;
③当$n > 2$时,此时$x = 0$时取得最大值,$x = n$时取得最小值,最大值为9,最小值为$-3n^{2}+9$,已知最大值与最小值的差为12,则$9 + 3n^{2}-9 = 12$,解得$n_{1}=-2,n_{2}=2$,但是这与假设矛盾,所以这种情况不符合题意,舍去.
$\therefore$综上,n的取值范围为$0\leqslant n\leqslant2$.故选:B.
①当$n < 0$时,当$-2\leqslant x\leqslant n$时,y随x的增大而增大,那么$x = - 2$时取得最小值,$x = n$时取得最大值,最小值为$-3$,最大值为$-3n^{2}+9$,则可列出方程:$-3n^{2}+9 + 3 = 12$,解得$n = 0$,但是这与假设矛盾,所以这种情况不符合题意,舍去;
②当$0\leqslant n\leqslant2$时,此时$x = 0$时取得最大值,$x = - 2$时取得最小值,最大值为9,最小值为$-3$,此时最大值与最小值的差为12,符合题意;
③当$n > 2$时,此时$x = 0$时取得最大值,$x = n$时取得最小值,最大值为9,最小值为$-3n^{2}+9$,已知最大值与最小值的差为12,则$9 + 3n^{2}-9 = 12$,解得$n_{1}=-2,n_{2}=2$,但是这与假设矛盾,所以这种情况不符合题意,舍去.
$\therefore$综上,n的取值范围为$0\leqslant n\leqslant2$.故选:B.
11. 抛物线$y = ax^{2}+x + 1$的开口向下,则 a 的值可以取
-1
.(写出一个即可)
答案:
11.$-1$(答案不唯一) 解析:由条件可知$a < 0$,不妨取$a = - 1$.
故答案为$-1$(答案不唯一).
故答案为$-1$(答案不唯一).
12. 若扇形的圆心角为$90^{\circ}$,半径为 2,则它的弧长为
π
.(结果保留$\pi$)
答案:
12.$\pi$ 解析:因为扇形的圆心角为$90^{\circ}$,半径为2,所以它的弧长为$\frac{90×\pi×2}{180}=\pi$.
故答案为$\pi$.
故答案为$\pi$.
13. 一根排水管的截面如图所示.已知排水管的半径$OB = 13\ cm$,水面宽$AB = 24\ cm$,则截面圆心 O 到水面的距离 OC 为
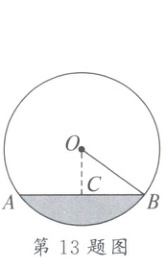
5
cm.
答案:
13.5 解析:由题意可得$BC = AC = \frac{1}{2}AB = 12$cm,
$\therefore OC = \sqrt{OB^{2}-BC^{2}}=\sqrt{13^{2}-12^{2}} = 5$cm.
故答案为5.
$\therefore OC = \sqrt{OB^{2}-BC^{2}}=\sqrt{13^{2}-12^{2}} = 5$cm.
故答案为5.
14. 如图,在半径为 3 的$\odot O$上,以 3 为半径依次截取六个点,并连结得六边形 ABCDEF,连结 AC,CE,则四边形 ACEF 的面积是
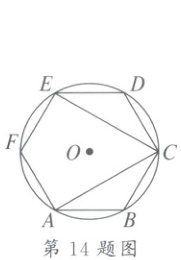
9√3
.
答案:
14.$9\sqrt{3}$ 解析:四边形ACEF的面积为$\frac{\sqrt{3}}{4}×3^{2}×(6 - 2)=9\sqrt{3}$.
故答案为$9\sqrt{3}$.
故答案为$9\sqrt{3}$.
15. 若抛物线$y = x^{2}+bx + c$经过点$(1,0)$,$(3,0)$,则 b 的值为
-4
.
答案:
15.$-4$ 解析:抛物线$y = x^{2}+bx + c$经过点$(1,0),(3,0)$,
$\therefore$抛物线对称轴为直线$x = 2$,$\therefore -\frac{b}{2}=2$,则$b = - 4$.
故答案为$-4$.
$\therefore$抛物线对称轴为直线$x = 2$,$\therefore -\frac{b}{2}=2$,则$b = - 4$.
故答案为$-4$.
16. 某大门是轴对称图形,由矩形与哥特式尖拱组成(如图 1),图 2 是其设计图,尖拱部分是两条等弧,圆心均落在直线 AB 上,圆弧的半径为$\frac{13}{4}$米,$CD = 4$米.过拱尖 P 作$PN\perp CD$分别交 AB,CD 于点 M,N.若$\frac{PM}{MN}=\frac{3}{5}$,则高 PN 等于
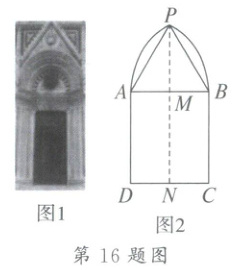
8
米.
答案:
16.8 解析:设$\overset{\frown}{AP}$的圆心为O,连结PO,则$OA = OP = \frac{13}{4}$米,
$\because$四边形ABCD是矩形,$\therefore AB = CD = 4$米,由轴对称知,$AM = BM = \frac{1}{2}AB = 2$米,
$\therefore OM = OA - AM=\frac{5}{4}$米.
$\because PM\perp AB$,$\therefore \angle PMO = 90^{\circ}$,$\therefore PM = \sqrt{OP^{2}-OM^{2}} = 3$米.
$\because \frac{PM}{MN}=\frac{3}{5}$,$\therefore MN = 5$米,$\therefore PN = 8$米.
故答案为8.

16.8 解析:设$\overset{\frown}{AP}$的圆心为O,连结PO,则$OA = OP = \frac{13}{4}$米,
$\because$四边形ABCD是矩形,$\therefore AB = CD = 4$米,由轴对称知,$AM = BM = \frac{1}{2}AB = 2$米,
$\therefore OM = OA - AM=\frac{5}{4}$米.
$\because PM\perp AB$,$\therefore \angle PMO = 90^{\circ}$,$\therefore PM = \sqrt{OP^{2}-OM^{2}} = 3$米.
$\because \frac{PM}{MN}=\frac{3}{5}$,$\therefore MN = 5$米,$\therefore PN = 8$米.
故答案为8.

查看更多完整答案,请扫码查看


