《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

1. $\cos 60^{\circ}$的值为(B)

A.$\frac{\sqrt{3}}{2}$
B.$\frac{1}{2}$
C.$\frac{\sqrt{3}}{3}$
D.$\sqrt{3}$

答案： 1.B　解析:$\cos 60° = \frac{1}{2}$.
　故选B.

2. 在$\triangle ABC$中，$\angle A$，$\angle B$，$\angle C$的对边分别为$a$，$b$，$c$。已知$a = 6$，$b = 8$，$c = 10$，则$\cos A$的值为(C)

A.$\frac{3}{5}$
B.$\frac{3}{4}$
C.$\frac{4}{5}$
D.$\frac{4}{3}$

答案： 2.C　解析:在$\triangle ABC$中，
　$\because a = 6,b = 8,c = 10,a^2 + b^2 = 6^2 + 8^2 = 36 + 64 = 100,c^2 = 100$.
　$\therefore a^2 + b^2 = c^2$.
　$\therefore \triangle ABC$是直角三角形.
　$\therefore \cos A = \frac{b}{c} = \frac{8}{10} = \frac{4}{5}$.
　故选C.

3. 在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，若$AB = 5$，$\cos B = \frac{4}{5}$，则$AC$等于(B)

A.$\frac{12}{5}$
B.3
C.4
D.5

答案：
3.B　解析:如图所示，
　$\because$在$Rt\triangle ABC$中$,\angle C = 90°$，
　　　　　　　　　　　　　　　　　
　$\therefore \cos B = \frac{4}{5} = \frac{BC}{AB}$，
　$\because AB = 5$，
　$\therefore BC = 4$，
　$\therefore AC = \sqrt{5^2 - 4^2} = 3$.
　故选B.

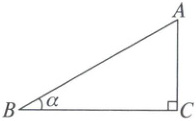
4. 如图，某商场大厅电梯的横截面示意图中，$AB$的长为12米，$AB$与$BC$的夹角为$\alpha$，则高$AC$为(A)

A.$12\sin \alpha$米
B.$12\cos \alpha$米
C.$\frac{12}{\sin \alpha}$米
D.$\frac{12}{\cos \alpha}$米

答案： 4.A　解析:由题意得$AC \perp BC$，
　在$Rt\triangle ABC$中$,AB = 12$米$,\angle ABC = \alpha$ ，
　$\therefore AC = AB · \sin\alpha = 12\sin\alpha$（米），
　故选A.

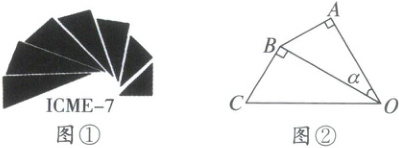
5. 图①是第七届国际数学教育大会(ICME)会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图②所示的四边形$OABC$。若$AB = BC = 1$，$\angle AOB = \alpha$，则$\tan \angle BOC$的值为(A)

A.$\sin \alpha$
B.$\cos \alpha$
C.$\tan \alpha$
D.$\frac{1}{\sin \alpha}$

答案： 5.A　解析:$\because AB = BC = 1$，
　在$Rt\triangle OAB$中$,\sin\alpha = \frac{AB}{OB}$，
　$\therefore OB = \frac{1}{\sin\alpha}$，
　在$Rt\triangle OBC$中$,\tan\angle BOC = \frac{BC}{OB} = \frac{1}{\frac{1}{\sin\alpha}} = \sin\alpha$.
　故选A.

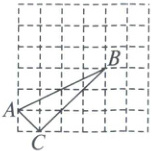
6. 如图，在正方形网格中有$\triangle ABC$，则$\sin \angle ABC$的值等于(B)

A.$\frac{3\sqrt{10}}{10}$
B.$\frac{\sqrt{10}}{10}$
C.$\frac{1}{3}$
D.$\sqrt{10}$

答案： 6.B　解析:$\because AB = \sqrt{20},BC = \sqrt{18},AC = \sqrt{2}$，
　$\therefore AB^2 = BC^2 + AC^2$，
　$\therefore \angle ACB = 90°$.
　$\therefore \sin\angle ABC = \frac{AC}{AB} = \frac{\sqrt{2}}{\sqrt{20}} = \frac{\sqrt{10}}{10}$.
　故选B.

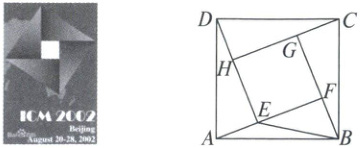
7. 第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”。如图，在由四个全等的直角三角形($\triangle DAE$，$\triangle ABF$，$\triangle BCG$，$\triangle CDH$)和中间一个小正方形$EFGH$拼成的大正方形$ABCD$中，$\angle ABF ＞ \angle BAF$，连结$BE$。设$\angle BAF = \alpha$，$\angle BEF = \beta$，若正方形$EFGH$与正方形$ABCD$的面积之比为$1 : n$，$\tan \alpha = \tan^2 \beta$，则$n =$(C)

A.5
B.4
C.3
D.2

答案： 7.C　解析:设$AE = a,DE = b$，则$BF = a,AF = b$，
　$\because \tan\alpha = \frac{a}{b},\tan\beta = \frac{a}{b - a},\tan\alpha = \tan^2\beta$，
　$\therefore \frac{a}{b} = \left( \frac{a}{b - a} \right)^2$，
　$\therefore (b - a)^2 = ab$，
　$\therefore a^2 + b^2 = 3ab$，
　$\because a^2 + b^2 = AD^2 = S_{正方形ABCD},S_{正方形EFGH} = (b - a)^2$，
　$\therefore S_{正方形EFGH} : S_{正方形ABCD} = ab : 3ab = 1 : 3$，
　$\because S_{正方形EFGH} : S_{正方形ABCD} = 1 : n$，
　$\therefore n = 3$.
　故选C.