《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

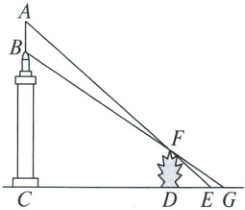
22. 如图，建筑物$BC$上有一根旗杆$AB$，小芳计划测量该建筑物的高度；方法如下：在该建筑物底部所在的平地上有一棵小树$FD$，小芳沿$CD$后退，发现地面上的点$E$、树顶$F$、旗杆顶端$A$恰好在一条直线上，继续后退，发现地面上的点$G$、树顶$F$、建筑物顶端$B$恰好在一条直线上，已知旗杆$AB = 3$米，$FD = 4$米，$DE = 5$米，$EG = 1.5$米，点$A$，$B$，$C$在一条直线上，点$C$，$D$，$E$，$G$在一条直线上，$AC$，$FD$均垂直于$CG$，请你帮助小芳求出这座建筑物的高$BC$。

答案： 22.解:由题意可得∠ACE=∠EDF=90°，∠AEC =∠FED，
∴△ACE∽△FDE，
∴$\frac{AC}{FD}$=$\frac{CE}{DE}$，
　　即$\frac{3+BC}{4}$=$\frac{CD+5}{5}$，
∴$CD=\frac{5BC-5}{4}$。
　　由题意可得∠BCG=∠FDG=90°，∠BGC=∠FGD，
∴△BCG∽△FDG，
∴$\frac{BC}{FD}$=$\frac{CG}{DG}$，
　　即$\frac{BC}{4}$=$\frac{CD+5+1.5}{5+1.5}$，
∴6.5BC=4(CD+6.5)，
∴$6.5BC=4 × \frac{5BC-5}{4}+26$，
∴BC=14米，
∴这座建筑物的高BC为14米。

23. 要在半径长为$1$米、圆心角为$60^{\circ}$的扇形$AOB$铁皮上截取一块尽可能大的正方形。小明设计如下两种截取方案。
方案一（如图1）：$C$在半径$OA$上，$D$，$E$在半径$OB$上，$F$在$\overset{\frown}{AB}$上；
方案二（如图2）：$C$在$OA$上，$D$在$OB$上，$E$，$F$在$\overset{\frown}{AB}$上。
请通过计算这两种方案中正方形铁皮的面积帮小明选择合理的方案。（参考数据：$\sqrt{2} \approx 1.41$，$\sqrt{3} \approx 1.73$）

答案：
23.解:方案一:如图1，连结OF，
　　设正方形CDEF的边长为x米，
∵圆心角为60°，
∴∠OCD=30°，
∴$OD=\frac{\sqrt{3}}{3}x$，
　　则在Rt△OFE中，
$OF^2=EF^2+OE^2$，
　　即$1^2=x^2+(x+\frac{\sqrt{3}}{3}x)^2$，
　解得$x^2=\frac{21-6\sqrt{3}}{37}$，
∴$S_{四边形CDEF}=x^2=\frac{21-6\sqrt{3}}{37} \approx 0.29$平方米；
　　
　　方案二:如图2，
　　过O作OG⊥EF，交CD于点H，连结OE，
　　设EG=y，
∵四边形CDEF是正方形，
∴OH⊥CD，
∴DH=EG=y，
∵∠DOC=60°，H为CD的中点，
∴$OH=\sqrt{3}CH$，
∴$OG=OH+HG=\sqrt{3}HC+CF=\sqrt{3}y+2y$，
　　在Rt△OEG中，
$OE^2=GE^2+OG^2$，即$1^2=y^2+(\sqrt{3}y+2y)^2$，
　　解得$y^2=\frac{2-\sqrt{3}}{4}$，
∴$S_{四边形CDEF}=4y^2=2-\sqrt{3} \approx 0.27$平方米。
∵0.27＜0.29，
∴第一种方案截取的正方形的面积最大。