《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

1. “抛一枚均匀硬币，落地后正面朝上”这一事件是(B)

A.必然事件
B.随机事件
C.确定事件
D.不可能事件

答案： 1.B 解析：抛一枚均匀硬币，落地后可能正面朝上，也可能反面朝上，故抛一枚均匀硬币，落地后正面朝上是随机事件.故选：B.

2. 若$2x = 3y$，则$\frac{x}{y}$的值为(C)

A.$\frac{2}{5}$
B.$\frac{2}{3}$
C.$\frac{3}{2}$
D.$\frac{5}{3}$

答案： 2.C 解析：
∵2x=3y，
∴$\frac{x}{y}=\frac{3}{2}$.故选：C.

3. 已知$\odot O$的半径为5，点$P$在$\odot O$外，则$OP$的长可能是(D)

A.3
B.4
C.5
D.6

答案： 3.D 解析：
∵⊙O的半径为5，点P在⊙O外，
∴OP＞5.故选：D.

4. 已知在圆内接四边形$ABCD$中，$\angle A:\angle B:\angle C = 2:3:7$.则$\angle B$的大小是(B)

A.$30^{\circ}$
B.$60^{\circ}$
C.$45^{\circ}$
D.$90^{\circ}$

答案： 4.B 解析：设∠A=2x，则∠B=3x，∠C=7x，
∵四边形ABCD是圆内接四边形，
∴∠A+∠C=180°，即2x+7x=180°，
解得x=20°，
∴∠B=3x=60°.故选：B.

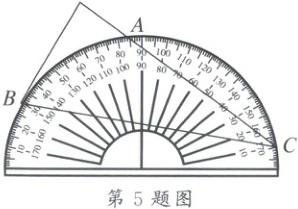
5. 将量角器按如图所示的方式放置在三角形纸板上，使点$C$在半圆上.点$A$，$B$的读数分别为$86^{\circ}$，$30^{\circ}$，则$\angle ACB$的大小为(A)

A.$28^{\circ}$
B.$30^{\circ}$
C.$43^{\circ}$
D.$60^{\circ}$

答案：
5.A 解析：连结OA，OB，如图.

由题意，∠AOB=86°−30°=56°，
∴∠ACB=$\frac{1}{2}$∠AOB=28°.故选：A.

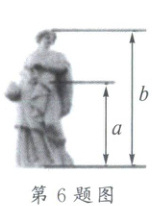
6. 生活中到处可见黄金分割的美.如图，在设计人体雕像时，使雕像的腰部以下$a$与全身$b$的高度比值接近$0.618$，可以增加视觉美感.若图中$b$为2米，则$a$约为(A)

A.$1.24$米
B.$1.38$米
C.$1.42$米
D.$1.62$米

答案： 6.A 解析：
∵雕像的腰部以下a与全身b的高度比值接近0.618，
∴$\frac{a}{b}$≈0.618，
∵b为2米，
∴a约为1.24米.故选：A.

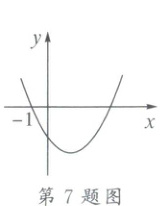
7. 如图，二次函数$y = ax^{2}-4ax + m$($m$为常数)的图象与$x$轴的一个交点为$(-1,0)$，则关于$x$的一元二次方程$ax^{2}-4ax + m = 0$($m$为常数)的两实数根是(B)

A.$x_{1}=-1$，$x_{2}=3$
B.$x_{1}=-1$，$x_{2}=5$
C.$x_{1}=1$，$x_{2}=-5$
D.$x_{1}=1$，$x_{2}=3$

答案： 7.B 解析：二次函数y=ax²−4ax+m（m为常数）的图象的对称轴为直线x=$-\frac{-4a}{2a}$=2，
∵二次函数y=ax²−4ax+m（m为常数）的图象与x轴的一个交点为(−1,0)，
∴二次函数y=ax²−4ax+m（m为常数）的图象与x轴的另一个交点为(5,0)，
∴关于x的一元二次方程ax²−4ax+m=0（m为常数）的两实数根是x₁=−1，x₂=5.
故选：B.

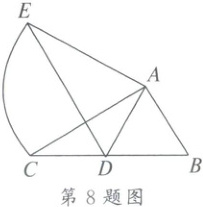
8. 如图，将$Rt\triangle ABC$以点$A$为中心顺时针旋转得到$\triangle ADE$，若点$B$的对应点$D$恰为$BC$边的中点，$AB = 1$，则$\overset{\frown}{CE}$的长为(C)

A.$\frac{\pi}{3}$
B.$\frac{\pi}{6}$
C.$\frac{\sqrt{3}\pi}{3}$
D.$\frac{\sqrt{3}\pi}{6}$

答案： 8.C 解析：根据旋转的性质，得AD=AB=1，
∵D是BC的中点，
∴BC=2AD=2，
在Rt△ABC中根据勾股定理，得AC=$\sqrt{BC²−AB²}$=$\sqrt{2²−1²}$=$\sqrt{3}$，
∵tan∠ABC=$\frac{AC}{AB}$=$\sqrt{3}$，
∴∠ABC=60°，
∴△ABD是等边三角形，
∴∠BAD=60°，
∵∠BAD+∠DAC=∠DAC+∠CAE=90°，
∴∠CAE=∠BAD=60°，
∴$\overset{\frown}{CE}$=$\frac{60π×\sqrt{3}}{180}$=$\frac{\sqrt{3}π}{3}$.故选：C.