《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

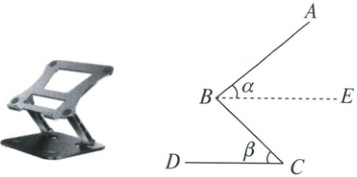
19. (8分)如图，一款可调节的笔记本电脑支架放置在水平桌面上，通过调节$BA$与$CB$的仰角$\alpha$与$\beta$的大小来调整个人舒适的高度，已知调节杆$CB = 11$cm，$AB = 20$cm，$AB$的最大仰角$\alpha$为$53^{\circ}$。
(1)当点$B$离桌面高度为5cm时，手腕最舒适，请问应该调整哪个角的大小？调整为多少度？
(2)在(1)的条件下，求点$A$到桌面的最大高度。(参考数据：$\sin 53^{\circ} \approx 0.80$，$\cos 53^{\circ} \approx 0.60$，$\tan 53^{\circ} \approx 1.33$，$\sin 27^{\circ} \approx 0.45$，$\cos 27^{\circ} \approx 0.89$)

答案：
19.解：
(1)如图，过点$B$作$BG \perp CD$于点$G$，

在$Rt\triangle BCG$中，$CB = 11 cm$，$BG = 5 cm$，$\therefore \sin \beta=\frac{BG}{CB}=\frac{5}{11} \approx 0.45$，$\therefore \beta \approx 27°$，答：应该调整$\beta$的大小，调整约为$27$度.
(2)如图，过点$A$作$AF \perp BE$于点$F$，
在$Rt\triangle ABF$中，$AF = AB · \sin \alpha = 20 · \sin 53° \approx 20 × 0.8 = 16(cm)$，$\therefore$点$A$到桌面的最大高度$=BG + AF = 21cm$.

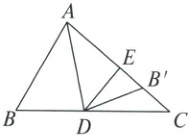
20. (8分)如图，在$\triangle ABC$中，点$D$，$E$分别在边$BC$，$AC$上，把$\triangle ABD$沿$AD$折叠，点$B$落在$AC$边上的$B'$处，把$\triangle CDE$沿$DE$折叠，点$C$恰好与点$A$重合。
(1)求证：$\triangle ABD \backsim \triangle CBA$；
(2)当$BD = 4$，$CD = 5$时，求$EB'$的长。

答案： 20.
(1)证明：$\because$把$\triangle ABD$沿$AD$折叠，点$B$落在$AC$边上的$B^\prime$处，$\therefore \angle DAB = \angle DAC$，$\because$把$\triangle CDE$沿$DE$折叠，点$C$恰好与点$A$重合，$\therefore \angle C = \angle DAC$，$\therefore \angle DAB = \angle C$，$\because \angle B = \angle B$，$\therefore \triangle ABD \sim \triangle CBA$.
(2)解：$\because BD = 4$，$CD = 5$，$\therefore BC = BD + CD = 4 + 5 = 9$，$\because \triangle ABD \sim \triangle CBA$，$\therefore \frac{BA}{BC}=\frac{BD}{BA}=\frac{AD}{CA}$，$\therefore BA^2 = BD · BC = 4 × 9 = 36$，$\therefore BA = 6$或$BA = -6$(不符合题意，舍去)，由折叠得$AD = CD = 5$，$B^\prime A = BA = 6$，$AE = CE$，$\therefore CA=\frac{BA · AD}{BD}=\frac{6 × 5}{4}=\frac{15}{2}$，$\therefore AE=\frac{1}{2}CA=\frac{1}{2} × \frac{15}{2}=\frac{15}{4}$，$\therefore EB^\prime=B^\prime A - AE = 6 - \frac{15}{4}=\frac{9}{4}$，$\therefore EB^\prime$的长是$\frac{9}{4}$.