《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

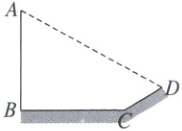
12. 阳光下，电线杆$AB$落在一段斜坡和水平地面上的影子分别是$CD$和$BC$，小亮量得$CD = 8m$，$BC = 20m$，斜坡$CD$的坡度为$1 : \sqrt{3}$，小亮的身高1.65m，此时他在水平地面上的影子长为3.3m，求电线杆的高度(结果保留根号)。

答案：
12.解:过点$D$作$DE \perp BC$交$BC$的延长线于点$E$，$DF \perp AB$于$F$，
　　则四边形$BFDE$为矩形，
　　$\therefore BF = DE,DF = BE$，
　　在$Rt\triangle DCE$中，斜坡$CD$的坡度为$1 : \sqrt{3}$，
　　则$\tan\angle DCE = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}$，
　　$\therefore \angle DCE = 30°$，
　　$\therefore DE = \frac{1}{2}CD = 4$m，$CE = CD · \cos\angle DCE = 8 × \frac{\sqrt{3}}{2} = 4\sqrt{3}$m，
　　$\therefore BF = DE = 4$m，$DF = BE = BC + CE = (20 + 4\sqrt{3})$m，
　　$\because$小亮的身高$1.65$m，此时他在水平地面上的影子长为$3.3$m，
　　$\therefore AF = \frac{1}{2}DF = (10 + 2\sqrt{3})$m，
　　$\therefore AB = AF + BF = (14 + 2\sqrt{3})$m.
答:电线杆的高度为$(14 + 2\sqrt{3})$m.