《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

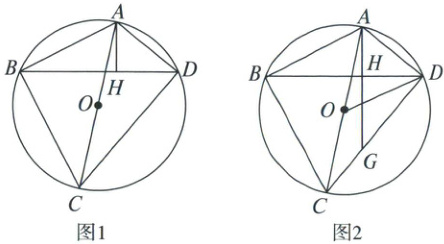
24. (12 分) 四边形 $ABCD$ 内接于 $\odot O$，$AC$ 为 $\odot O$ 的直径，连结 $BD$，过 $A$ 作 $AH \perp BD$ 于点 $H$。
（1）如图 1，求证：$\angle BAC = \angle DAH$；
（2）如图 2，延长 $AH$ 交 $CD$ 于点 $G$，连结 $OD$，且 $OD // AB$。
① 求证：$BD = CD$；
② 若 $\cos\angle BAC = \frac{3}{5}$，$AH = 3$，求 $CG$ 的长。

答案：
24.
(1)证明：$\because AC$为$\odot O$的直径，$AH\perp BD$于点H，$\therefore \angle ABC = \angle AHD = 90°$，$\therefore \angle BAC + \angle ACB = 90°$，$\angle DAH + \angle ADB = 90°$。$\because \angle ACB = \angle ADB$，$\therefore \angle BAC = \angle DAH$。
(2)①证明：$\because OD// AB$，$\therefore \angle AOD = \angle BAC$。$\because \angle BAC = \angle BDC$，$\therefore \angle AOD = \angle BDC$。$\because \angle OAD = \angle DBC$，$\therefore \triangle OAD\sim \triangle DBC$，$\therefore \angle ODA = \angle DCB$。$\because OD = OA$，$\therefore \angle OAD = \angle ODA$，$\therefore \angle DBC = \angle DCB$，$\therefore BD = CD$。
②解：如图，作$DL\perp AC$于点L，则$\angle OLD = \angle ALD = \angle ADC = 90°$。$\because \angle ABC = \angle AHD = 90°$，$\angle BAC = \angle DAH$，$\therefore \frac{AD}{AG} = \frac{AH}{AD} = \cos \angle DAH = \cos \angle BAC = \frac{3}{5}$。$\because AH = 3$，$\therefore AD = \frac{5}{3}AH = \frac{5}{3}× 3 = 5$，$\therefore AG = \frac{5}{3}AD = \frac{5}{3}× 5 = \frac{25}{3}$，$\therefore DG = \sqrt{AG^2 - AD^2} = \sqrt{(\frac{25}{3})^2 - 5^2} = \frac{20}{3}$。设$OD = OA = 5m$，$\because \angle AOD = \angle BAC$，$\therefore \frac{OL}{OD} = \cos \angle AOD = \cos \angle BAC = \frac{3}{5}$，$\therefore OL = \frac{3}{5}OD = \frac{3}{5}× 5 = 3m$，$\therefore AL = OA - OL = 5m - 3m = 2m$，$DL = \sqrt{OD^2 - OL^2} = \sqrt{(5m)^2 - (3m)^2} = 4m$。$\because \frac{CD}{AD} = \frac{DL}{AL} = \tan \angle CAD = \frac{4m}{2m} = 2$，$\therefore CD = 2AD = 2× 5 = 10$，$\therefore CG = CD - DG = 10 - \frac{20}{3} = \frac{10}{3}$，$\therefore CG$的长是$\frac{10}{3}$。