第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
23. (8分)我们规定:在平面直角坐标系中,若一个点的横坐标与纵坐标互为相反数,则这个点叫做“$ M $点”。如 $ P ( 2, - 2 ) $ 就是“$ M $点”。
(1)任意写一个二次函数,使它的图象上存在“$ M $点”;
(2)已知二次函数 $ y = x ^ { 2 } - m x - 3 $。
① 求证:该函数图象上一定存在两个“$ M $点”;
② 若这两个“$ M $点”的横坐标分别是 $ x _ { 1 } $,$ x _ { 2 } $,且 $ x _ { 1 } < 1 < x _ { 2 } $,求 $ m $ 的取值范围。
(1)任意写一个二次函数,使它的图象上存在“$ M $点”;
(2)已知二次函数 $ y = x ^ { 2 } - m x - 3 $。
① 求证:该函数图象上一定存在两个“$ M $点”;
② 若这两个“$ M $点”的横坐标分别是 $ x _ { 1 } $,$ x _ { 2 } $,且 $ x _ { 1 } < 1 < x _ { 2 } $,求 $ m $ 的取值范围。
答案:
23.
(1)解:由题知,这个二次函数表达式可以是$y = x^2$(答案不唯一).
(2)①证明:由“$M$点”的定义可知,“$M$点”坐标为$(x,-x)$,将$(x,-x)$代入$y = x^2 - mx - 3$,得$x^2 - mx - 3=-x$,则$x^2+(1 - m)x - 3 = 0$.
∵$\Delta=(1 - m)^2 - 4×1×(-3)=(m - 1)^2 + 12>0$,
∴此方程有两个不相等的实数根,
∴该函数图象上一定存在两个“$M$点”.
②解:
∵这两个“$M$点”的横坐标分别是$x_1$,$x_2$,且$x_1<1<x_2$,
∴$(x_1 - 1)(x_2 - 1)<0$,即$x_1x_2-(x_1 + x_2)+1<0$.由$x^2+(1 - m)x - 3 = 0$,得$x_1 + x_2=m - 1$,$x_1x_2=-3$,所以$-3-(m - 1)+1<0$,解得$m>-1$,所以$m$的取值范围是$m>-1$.
(1)解:由题知,这个二次函数表达式可以是$y = x^2$(答案不唯一).
(2)①证明:由“$M$点”的定义可知,“$M$点”坐标为$(x,-x)$,将$(x,-x)$代入$y = x^2 - mx - 3$,得$x^2 - mx - 3=-x$,则$x^2+(1 - m)x - 3 = 0$.
∵$\Delta=(1 - m)^2 - 4×1×(-3)=(m - 1)^2 + 12>0$,
∴此方程有两个不相等的实数根,
∴该函数图象上一定存在两个“$M$点”.
②解:
∵这两个“$M$点”的横坐标分别是$x_1$,$x_2$,且$x_1<1<x_2$,
∴$(x_1 - 1)(x_2 - 1)<0$,即$x_1x_2-(x_1 + x_2)+1<0$.由$x^2+(1 - m)x - 3 = 0$,得$x_1 + x_2=m - 1$,$x_1x_2=-3$,所以$-3-(m - 1)+1<0$,解得$m>-1$,所以$m$的取值范围是$m>-1$.
24. (8分)如图1,在 $ \triangle ABC $ 中,$ \angle A C B = 90 ^ { \circ } $,$ A C = B C $,点 $ D $,$ E $ 分别在 $ AB $,$ BC $ 边上,且 $ \angle C D E = 45 ^ { \circ } $。经过点 $ C $,$ D $,$ E $ 的 $ \odot O $ 分别交 $ AC $,$ AB $ 边于点 $ F $,$ G $,连结 $ DF $。
(1)求证:$ C F = C E $;
(2)若 $ A B = 6 \sqrt { 2 } $,$ D F = 2 D E $,求 $ C E $ 的长;
(3)如图2,连结 $ CG $,若 $ C G // D E $,请直接写出 $ \frac { C E } { B E } $ 的值。
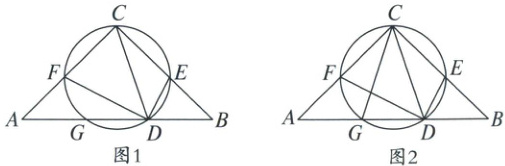
(1)求证:$ C F = C E $;
(2)若 $ A B = 6 \sqrt { 2 } $,$ D F = 2 D E $,求 $ C E $ 的长;
(3)如图2,连结 $ CG $,若 $ C G // D E $,请直接写出 $ \frac { C E } { B E } $ 的值。

答案:
24.
(1)证明:如图,连结$EF$,

∵$\angle CDE = 45^{\circ}$,$\angle CDE=\angle CFE$,
∴$\angle CFE = 45^{\circ}$,
∵$\angle ECF = 90^{\circ}$,
∴$\triangle ECF$是等腰直角三角形,
∴$CF = CE$.
(2)解:如图,
∵$\angle ACB = 90^{\circ}$,$AC = BC$,
∴$AB=\sqrt{2}AC$,
∵$AB = 6\sqrt{2}$,
∴$AC = BC = 6$,设$DE = a$,则$DF = 2a$,
∵$\angle ECF = 90^{\circ}$,
∴$EF$是$\odot O$的直径,
∴$\angle FDE = 90^{\circ}$,
∴$EF=\sqrt{5}a$,
∵$\triangle ECF$是等腰直角三角形,
∴$CE = CF=\frac{\sqrt{5}a}{\sqrt{2}}=\frac{\sqrt{10}}{2}a$,
∵$C$,$F$,$D$,$E$四点共圆,
∴$\angle CFD+\angle CED = 180^{\circ}$,
∵$\angle AFD+\angle CFD = 180^{\circ}$,
∴$\angle AFD=\angle CED$,
∵$\angle A=\angle CDE = 45^{\circ}$,
∴$\triangle AFD∽\triangle DEC$,
∴$\frac{AF}{DE}=\frac{DF}{CE}$,即$\frac{6-\frac{\sqrt{10}}{2}a}{a}=\frac{2a}{\frac{\sqrt{10}}{2}a}$,
∴$a=\frac{2\sqrt{10}}{3}$,经检验:$a=\frac{2\sqrt{10}}{3}$是原方程的解,
∴$CE=\frac{\sqrt{10}}{2}a=\frac{\sqrt{10}}{2}×\frac{2\sqrt{10}}{3}=\frac{10}{3}$.
(3)解:
∵$C$,$G$,$D$,$E$四点共圆,
∴$\angle BED=\angle CGD$,
∵$CG// DE$,
∴$\angle BDE=\angle CGD$,$CE = DG$,
∴$\angle BED=\angle BDE$,$CE = DG$,
∴$BD = BE$,
∴$CE + BE=DG + BD$,即$BC = BG = AC$,设$AC = BC = y$,则$AB=\sqrt{2}y$,
∴$AG = AB - BG=\sqrt{2}y - y=(\sqrt{2}-1)y$,由
(2)知$\triangle AFD∽\triangle DEC$,
∴$\angle ADF=\angle DCE$,
∵$\angle ACG=\angle ADF$
24.
(1)证明:如图,连结$EF$,

∵$\angle CDE = 45^{\circ}$,$\angle CDE=\angle CFE$,
∴$\angle CFE = 45^{\circ}$,
∵$\angle ECF = 90^{\circ}$,
∴$\triangle ECF$是等腰直角三角形,
∴$CF = CE$.
(2)解:如图,
∵$\angle ACB = 90^{\circ}$,$AC = BC$,
∴$AB=\sqrt{2}AC$,
∵$AB = 6\sqrt{2}$,
∴$AC = BC = 6$,设$DE = a$,则$DF = 2a$,
∵$\angle ECF = 90^{\circ}$,
∴$EF$是$\odot O$的直径,
∴$\angle FDE = 90^{\circ}$,
∴$EF=\sqrt{5}a$,
∵$\triangle ECF$是等腰直角三角形,
∴$CE = CF=\frac{\sqrt{5}a}{\sqrt{2}}=\frac{\sqrt{10}}{2}a$,
∵$C$,$F$,$D$,$E$四点共圆,
∴$\angle CFD+\angle CED = 180^{\circ}$,
∵$\angle AFD+\angle CFD = 180^{\circ}$,
∴$\angle AFD=\angle CED$,
∵$\angle A=\angle CDE = 45^{\circ}$,
∴$\triangle AFD∽\triangle DEC$,
∴$\frac{AF}{DE}=\frac{DF}{CE}$,即$\frac{6-\frac{\sqrt{10}}{2}a}{a}=\frac{2a}{\frac{\sqrt{10}}{2}a}$,
∴$a=\frac{2\sqrt{10}}{3}$,经检验:$a=\frac{2\sqrt{10}}{3}$是原方程的解,
∴$CE=\frac{\sqrt{10}}{2}a=\frac{\sqrt{10}}{2}×\frac{2\sqrt{10}}{3}=\frac{10}{3}$.
(3)解:
∵$C$,$G$,$D$,$E$四点共圆,
∴$\angle BED=\angle CGD$,
∵$CG// DE$,
∴$\angle BDE=\angle CGD$,$CE = DG$,
∴$\angle BED=\angle BDE$,$CE = DG$,
∴$BD = BE$,
∴$CE + BE=DG + BD$,即$BC = BG = AC$,设$AC = BC = y$,则$AB=\sqrt{2}y$,
∴$AG = AB - BG=\sqrt{2}y - y=(\sqrt{2}-1)y$,由
(2)知$\triangle AFD∽\triangle DEC$,
∴$\angle ADF=\angle DCE$,
∵$\angle ACG=\angle ADF$
查看更多完整答案,请扫码查看


