第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
在平面直角坐标系$xOy$中,已知抛物线$y=ax^{2}-2ax+a+3(a<0)$与$x$轴分别交于点$A$和点$B$,与$y$轴交于点$C$。
(1)如图1,若点$A$的坐标为$(-1,0)$,求抛物线的表达式和点$C$的坐标;
(2)过点$C$作$y$轴的垂线$l$,将抛物线在$y$轴右侧的部分沿直线$l$翻折,将翻折得到的图象与原抛物线剩余部分的图象组成新的图形,记为图形$G$。
①在(1)的条件下,在图形$G$位于$x$轴上方的部分是否存在点$D$,使得$S_{\triangle ABD}=3$?若存在,求点$D$的坐标;若不存在,请说明理由;
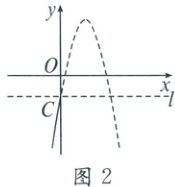
②如图2,已知点$P(1+a,p)$和点$Q(1-a,q)$是图形$G$上的点。设$t=p+q$,当$-3\leq t\leq0$时,请直接写出$a$的取值范围。

(1)如图1,若点$A$的坐标为$(-1,0)$,求抛物线的表达式和点$C$的坐标;
(2)过点$C$作$y$轴的垂线$l$,将抛物线在$y$轴右侧的部分沿直线$l$翻折,将翻折得到的图象与原抛物线剩余部分的图象组成新的图形,记为图形$G$。
①在(1)的条件下,在图形$G$位于$x$轴上方的部分是否存在点$D$,使得$S_{\triangle ABD}=3$?若存在,求点$D$的坐标;若不存在,请说明理由;
②如图2,已知点$P(1+a,p)$和点$Q(1-a,q)$是图形$G$上的点。设$t=p+q$,当$-3\leq t\leq0$时,请直接写出$a$的取值范围。


答案:
23.解:
(1)将A(−1,0)代入y=ax²−2ax+a+3,得a+2a+a+3=0,
解得a=−$\frac{3}{4}$,
∴抛物线的表达式为y=−$\frac{3}{4}$x²+$\frac{3}{2}$x+$\frac{9}{4}$,
令x=0,得y=$\frac{9}{4}$,
∴C(0,$\frac{9}{4}$).
(2)①存在点D,使得S_△ABD=3,理由如下:如图1,

在y=−$\frac{3}{4}$x²+$\frac{3}{2}$x+$\frac{9}{4}$中,令y=0得−$\frac{3}{4}$x²+$\frac{3}{2}$x +$\frac{9}{4}$=0,
解得x₁=−1,x₂=3,
∴A(−1,0),B(3,0),
∴AB=4.
∵y=−$\frac{3}{4}$x²+$\frac{3}{2}$x+$\frac{9}{4}$=−$\frac{3}{4}$(x−1)²+3,
∴顶点为(1,3),
过点C作y轴的垂线l:y=$\frac{9}{4}$,将抛物线在y轴右侧的部分沿直线l翻折,其余部分不变,得到y=$\frac{3}{4}$(x−1)²+$\frac{3}{2}$,
∴图形G的函数表达式为
$y = \begin{cases} -\frac{3}{4}(x - 1)^{2}+3(x\leq0)\frac{3}{4}(x - 1)^{2}+\frac{3}{2}(x>0)\end{cases}$
若x轴上方的图形G上存在点D,使得S_△ABD=$\frac{1}{2}$AB·y_D=3,则y_D=$\frac{3}{2}$,
当x<0时,将y=$\frac{3}{2}$代入y=−$\frac{3}{4}$(x−1)²+3,得−$\frac{3}{4}$(x−1)²+3=$\frac{3}{2}$,
解得x₁=$\sqrt{2}$+1(舍去),x₂=−$\sqrt{2}$+1;
∴此时D(−$\sqrt{2}$+1,$\frac{3}{2}$).
当x>0时,将y=$\frac{3}{2}$代入y=$\frac{3}{4}$(x−1)²+$\frac{3}{2}$,得$\frac{3}{4}$(x−1)²+$\frac{3}{2}$=$\frac{3}{2}$,解得x=1,
∴此时D(1,$\frac{3}{2}$).
综上,存在点D,使得S_△ABD=3,点D的坐标为(−$\sqrt{2}$+1,$\frac{3}{2}$)或(1,$\frac{3}{2}$).
②在y=ax²−2ax+a+3(a<0)中,令x=0,
得y=a+3,
∴C(0,a+3),
∴直线l:y=a+3,
∵y=ax²−2ax+a+3=a(x−1)²+3,
∴抛物线的顶点为(1,3).
将抛物线y=ax²−2ax+a+3(a<0)在y轴右侧的部分沿直线l翻折,得y=−a(x−1)²+2a+3,
∵点P(1+a,p)和点Q(1−a,q)是图形G上的点,
∴当a≤−1时,1+a≤0,1−a≥2,
即点P在y轴左侧,点Q在y轴右侧,如图2,

∴p=a²+3,q=−a²+2a+3,
∴t=p+q=2a+6,
∵−3≤t≤0,
∴−3≤2a+6≤0,
∴−$\frac{9}{2}$≤a≤−3;
当−1<a<0时,0<1+a<1,1<1−a<2,
即点P,Q均在y轴右侧,
∴2a+3<p<a+3,2a+3<q<a+3,
∴4a+6<p+q<2a+6,
∵−3≤t≤0,
∴−3≤p+q≤0,
$\begin{cases}4a + 6>-3\\2a + 6<0\end{cases}$
此不等式组无解,即−1<a<0不成立;
综上,a的取值范围为−$\frac{9}{2}$≤a≤−3.
23.解:
(1)将A(−1,0)代入y=ax²−2ax+a+3,得a+2a+a+3=0,
解得a=−$\frac{3}{4}$,
∴抛物线的表达式为y=−$\frac{3}{4}$x²+$\frac{3}{2}$x+$\frac{9}{4}$,
令x=0,得y=$\frac{9}{4}$,
∴C(0,$\frac{9}{4}$).
(2)①存在点D,使得S_△ABD=3,理由如下:如图1,

在y=−$\frac{3}{4}$x²+$\frac{3}{2}$x+$\frac{9}{4}$中,令y=0得−$\frac{3}{4}$x²+$\frac{3}{2}$x +$\frac{9}{4}$=0,
解得x₁=−1,x₂=3,
∴A(−1,0),B(3,0),
∴AB=4.
∵y=−$\frac{3}{4}$x²+$\frac{3}{2}$x+$\frac{9}{4}$=−$\frac{3}{4}$(x−1)²+3,
∴顶点为(1,3),
过点C作y轴的垂线l:y=$\frac{9}{4}$,将抛物线在y轴右侧的部分沿直线l翻折,其余部分不变,得到y=$\frac{3}{4}$(x−1)²+$\frac{3}{2}$,
∴图形G的函数表达式为
$y = \begin{cases} -\frac{3}{4}(x - 1)^{2}+3(x\leq0)\frac{3}{4}(x - 1)^{2}+\frac{3}{2}(x>0)\end{cases}$
若x轴上方的图形G上存在点D,使得S_△ABD=$\frac{1}{2}$AB·y_D=3,则y_D=$\frac{3}{2}$,
当x<0时,将y=$\frac{3}{2}$代入y=−$\frac{3}{4}$(x−1)²+3,得−$\frac{3}{4}$(x−1)²+3=$\frac{3}{2}$,
解得x₁=$\sqrt{2}$+1(舍去),x₂=−$\sqrt{2}$+1;
∴此时D(−$\sqrt{2}$+1,$\frac{3}{2}$).
当x>0时,将y=$\frac{3}{2}$代入y=$\frac{3}{4}$(x−1)²+$\frac{3}{2}$,得$\frac{3}{4}$(x−1)²+$\frac{3}{2}$=$\frac{3}{2}$,解得x=1,
∴此时D(1,$\frac{3}{2}$).
综上,存在点D,使得S_△ABD=3,点D的坐标为(−$\sqrt{2}$+1,$\frac{3}{2}$)或(1,$\frac{3}{2}$).
②在y=ax²−2ax+a+3(a<0)中,令x=0,
得y=a+3,
∴C(0,a+3),
∴直线l:y=a+3,
∵y=ax²−2ax+a+3=a(x−1)²+3,
∴抛物线的顶点为(1,3).
将抛物线y=ax²−2ax+a+3(a<0)在y轴右侧的部分沿直线l翻折,得y=−a(x−1)²+2a+3,
∵点P(1+a,p)和点Q(1−a,q)是图形G上的点,
∴当a≤−1时,1+a≤0,1−a≥2,
即点P在y轴左侧,点Q在y轴右侧,如图2,

∴p=a²+3,q=−a²+2a+3,
∴t=p+q=2a+6,
∵−3≤t≤0,
∴−3≤2a+6≤0,
∴−$\frac{9}{2}$≤a≤−3;
当−1<a<0时,0<1+a<1,1<1−a<2,
即点P,Q均在y轴右侧,
∴2a+3<p<a+3,2a+3<q<a+3,
∴4a+6<p+q<2a+6,
∵−3≤t≤0,
∴−3≤p+q≤0,
$\begin{cases}4a + 6>-3\\2a + 6<0\end{cases}$
此不等式组无解,即−1<a<0不成立;
综上,a的取值范围为−$\frac{9}{2}$≤a≤−3.
查看更多完整答案,请扫码查看


