《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

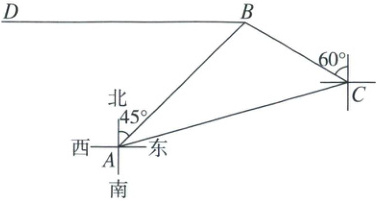
15. “和平使命”系列军演是具有战略影响的国际联合军事演习。在一次行动中，我军主力部队在$A$发现敌军在我军的东北方向的$B$处，遂立即通知位于我军北偏东$75^{\circ}$，距离$(6\sqrt{6} + 6\sqrt{2})km$，在$C$处执行任务的侦查小队，侦查小队测得敌军在北偏西$60^{\circ}$，迅速沿着路线$CA$向我军靠近，并在途中选取距离敌军最近的地方对敌军进行监测活动。
(1) 求点$B$到路线$CA$的最短距离；(精确到$0.1km$，参考数据：$\sqrt{2} \approx 1.414$，$\sqrt{3} \approx 1.732$)
(2) 上午$6:00$时，我军发现敌军开始沿$BD$向正西方向以$6km/h$的速度行进，敌军现有探测设备的有效侦测半径为$15km$，请问在敌军行进过程中，我军主力部队所在$A$地是否在敌军侦测范围内？如果在，我军需要从什么时间开始进行战略隐蔽，什么时间即可结束战略隐蔽？

答案：
15.解:
(1)如图，过点$B$作$BE \perp AC$于点$E$，
　　根据题意可知$\angle BAC = 75° - 45° = 30°,\angle BCA = 30° + 15° = 45°$，
　　$\therefore BE = CE,AB = 2BE$，
　　设$BE = CE = x$km，则$AE = \sqrt{3}x$km，
　　$\because AE + EC = AC = (6\sqrt{6} + 6\sqrt{2})$km，
　　$\therefore \sqrt{3}x + x = 6\sqrt{6} + 6\sqrt{2}$，
　　$\therefore x = 6\sqrt{2} \approx 8.5$km，
　　$\therefore BE \approx 8.5$km，
　　$\therefore$点$B$到路线$CA$的最短距离约为$8.5$km.
　　　　　　　　　
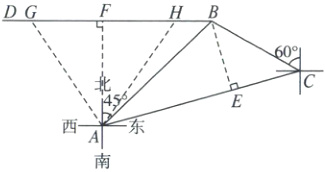
(2)$\because$点$B$到路线$CA$的最短距离为$BE$的长度等于$6\sqrt{2}$km，
　　$AB = 2BE = 12\sqrt{2}$km$＞ 15$km，
　　$\therefore$此时我军主力部队所在$A$地不在敌军的侦测范围内.
　　如图，过点$A$作$AF \perp BD$于点$F$，
　　$\because \angle FBA = 45°$，
　　$\therefore AF = \frac{\sqrt{2}}{2}AB = \frac{\sqrt{2}}{2} × 12\sqrt{2} = 12$（km），
　　$\therefore$此时我军主力部队所在$A$地在敌军的侦测范围，设在点$F$两侧的$GH$之间距离范围内，
　　根据题意可知$AH = AG = 15$km，
　　$\therefore FH = \sqrt{AH^2 - AF^2} = \sqrt{15^2 - 12^2} = 9$km，
　　$\therefore GF = 9$km，
　　$\therefore BH = BF - FH = AF - FH = 12 - 9 = 3$km，
　　$\therefore BG = 2FH + BH = 18 + 3 = 21$（km），
　　$\therefore t_1 = \frac{BH}{6} = 0.5$h，$t_2 = \frac{BG}{6} = \frac{21}{6} = 3.5$h.
　　$\therefore$我军需要从$6$点$30$分开始进行战略隐蔽，$9$点$30$分即可结束战略隐蔽.