第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
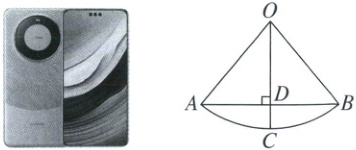
18. 某品牌手机系列完成了核心技术领域从0到1的跃迁,让无数国人为之自豪并被赞誉为“争气机”。手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量。圆弧对应的弦AB长80mm,弓形高CD长14mm求半径OA的长。

答案:
18.解:设半径OA的长为$r$mm,
则OA=OC=OB=$r$mm,
∵弓形高CD=14mm,
∴OD=($r$−14)mm.
∵OC⊥AB,AB=80mm,
∴$AD=\frac{1}{2}AB=40$mm,
在Rt△OAD中,由勾股定理,得$OA^{2}-OD^{2}=AD^{2}$,即$r^{2}-(r-14)^{2}=40^{2}$,
解得$r=\frac{449}{7}$.
答:半径OA的长为$\frac{449}{7}$mm.
则OA=OC=OB=$r$mm,
∵弓形高CD=14mm,
∴OD=($r$−14)mm.
∵OC⊥AB,AB=80mm,
∴$AD=\frac{1}{2}AB=40$mm,
在Rt△OAD中,由勾股定理,得$OA^{2}-OD^{2}=AD^{2}$,即$r^{2}-(r-14)^{2}=40^{2}$,
解得$r=\frac{449}{7}$.
答:半径OA的长为$\frac{449}{7}$mm.
19. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3)。
(1)若△ABC和△A₁B₁C₁关于x轴成轴对称,画出△A₁B₁C₁;
(2)点C₁的坐标为
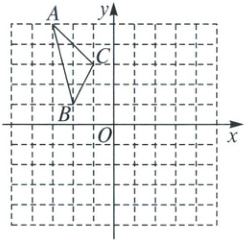
(1)若△ABC和△A₁B₁C₁关于x轴成轴对称,画出△A₁B₁C₁;
(2)点C₁的坐标为
(-1,-3)
,△ABC的面积为3
。
答案:
19.解:
(1)如图,△$A_{1}B_{1}C_{1}$为所作.
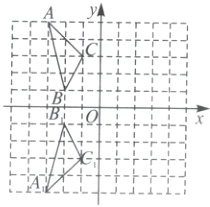
(2)点$C_{1}$的坐标为(-1,-3),△ABC的面积=$2×4-\frac{1}{2}×2×2-\frac{1}{2}×2×1-\frac{1}{2}×4×1=3$.
故答案为(-1,-3),3.
19.解:
(1)如图,△$A_{1}B_{1}C_{1}$为所作.

(2)点$C_{1}$的坐标为(-1,-3),△ABC的面积=$2×4-\frac{1}{2}×2×2-\frac{1}{2}×2×1-\frac{1}{2}×4×1=3$.
故答案为(-1,-3),3.
20. 如图,⊙O的直径BC为6cm,弦AC为3cm,∠CAB的平分线交⊙O于点D。
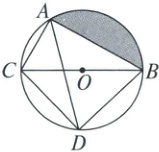
(1)求∠CBD的度数;
(2)求阴影部分的面积。

(1)求∠CBD的度数;
(2)求阴影部分的面积。
答案:
20.解:
(1)
∵BC是⊙O的直径,
∴∠CAB=90°.
∵AD平分∠CAB,
∴∠CAD=$\frac{1}{2}$∠CAB=45°,
∴∠CBD=∠CAD=45°.
(2)如图,连结OA,
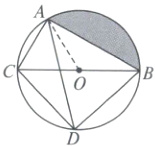
∵BC=6cm,AC=3cm,∠CAB=90°,
∴∠ABC=30°,OA=OB=3cm,$AB=\sqrt{6^{2}-3^{2}}=3\sqrt{3}$(cm),
∴∠ACB=90°−30°=60°,
∴∠AOB=2∠ACB=120°,
∴$S_{扇形AOB}=\frac{120\pi×3^{2}}{360}=3\pi(cm^{2})$.
∵OB=OC,
∴$S_{\triangle AOB}=\frac{1}{2}S_{\triangle ACB}=\frac{1}{2}×\frac{1}{2}×3×3\sqrt{3}=\frac{9\sqrt{3}}{4}(cm^{2})$,
∴$S_{阴影}=S_{扇形AOB}-S_{\triangle AOB}=(3\pi-\frac{9\sqrt{3}}{4})cm^{2}$,
即阴影部分的面积为$(3\pi-\frac{9\sqrt{3}}{4})cm^{2}$.
20.解:
(1)
∵BC是⊙O的直径,
∴∠CAB=90°.
∵AD平分∠CAB,
∴∠CAD=$\frac{1}{2}$∠CAB=45°,
∴∠CBD=∠CAD=45°.
(2)如图,连结OA,

∵BC=6cm,AC=3cm,∠CAB=90°,
∴∠ABC=30°,OA=OB=3cm,$AB=\sqrt{6^{2}-3^{2}}=3\sqrt{3}$(cm),
∴∠ACB=90°−30°=60°,
∴∠AOB=2∠ACB=120°,
∴$S_{扇形AOB}=\frac{120\pi×3^{2}}{360}=3\pi(cm^{2})$.
∵OB=OC,
∴$S_{\triangle AOB}=\frac{1}{2}S_{\triangle ACB}=\frac{1}{2}×\frac{1}{2}×3×3\sqrt{3}=\frac{9\sqrt{3}}{4}(cm^{2})$,
∴$S_{阴影}=S_{扇形AOB}-S_{\triangle AOB}=(3\pi-\frac{9\sqrt{3}}{4})cm^{2}$,
即阴影部分的面积为$(3\pi-\frac{9\sqrt{3}}{4})cm^{2}$.
查看更多完整答案,请扫码查看


