《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

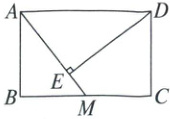
20. 如图，在矩形$ABCD$中，$AB = 2$，$BC = 3$，$M$是$BC$的中点，$DE \perp AM$于点$E$。
（1）求证：$\triangle ADE \backsim \triangle MAB$；
（2）求$DE$的长。

答案： 20.
(1)证明:
∵在矩形ABCD中，DE⊥AM于点E，
∴∠B=90°，∠BAD=90°，∠DEA=90°，
∴∠BAM+∠EAD=90°，∠EDA+∠EAD=90°，
∴∠BAM=∠EDA。
　　在△ADE和△MAB中，
∵∠AED=∠B，∠EDA =∠BAM，
∴△ADE∽△MAB。
(2)解:
∵在矩形ABCD中，AB=2，BC=3，M是BC的中点，
∴BM=$\frac{3}{2}$，
∴$AM=\sqrt{2^2+(\frac{3}{2})^2}$=$\frac{5}{2}$。
　　由
(1)知，△ADE∽△MAB，
∴$\frac{AM}{DA}$=$\frac{AB}{DE}$，
∴$\frac{\frac{5}{2}}{3}$=$\frac{2}{DE}$，
　　解得$DE=\frac{12}{5}$。

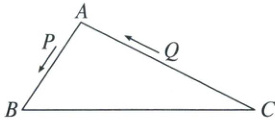
21. 如图，在$\triangle ABC$中，$AB = 8\ cm$，$AC = 16\ cm$，点$P$从$A$出发，以每秒$2\ cm$的速度向$B$运动，点$Q$从$C$同时出发，以每秒$3\ cm$的速度向$A$运动，其中一个动点到端点时，另一个动点也相应停止运动，那么，当以$A$，$P$，$Q$为顶点的三角形与$\triangle ABC$相似时，运动时间是多少？

答案： 21.解:设运动了t s，
　　根据题意，得AP=2t cm，CQ=3t cm，
　　则AQ=AC−CQ=(16−3t)cm。
　　当△APQ∽△ABC时，$\frac{AP}{AB}$=$\frac{AQ}{AC}$，
　　即$\frac{2t}{8}$=$\frac{16−3t}{16}$，
解得$t=\frac{16}{7}$；
　　当△APQ∽△ACB时，$\frac{AP}{AC}$=$\frac{AQ}{AB}$，
　　即$\frac{2t}{16}$=$\frac{16−3t}{8}$，
　　解得t=4。
　　故当以A、P、Q为顶点的三角形与△ABC相似时，运动时间是$\frac{16}{7}$s或4s。