《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

9. 在平面直角坐标系中，设函数 $ y_1 = x^2 + ax + b $，$ y_2 = -x^2 + bx + a $。（ ）

A.若 $ a ＞ b $，则函数 $ y_1 $ 和 $ y_2 $ 的图象有两个交点
B.若函数 $ y_1 $ 和 $ y_2 $ 的值互为相反数，则 $ x = -1 $
C.当 $ x = 1 $ 时，函数 $ y_1 $ 和 $ y_2 $ 的值相等
D.函数 $ y_1 $ 和 $ y_2 $ 的图象必经过同一个定点

答案： 9.A 解析：由题意，对于A，令$y_{1}=y_{2}$，$\therefore x^{2}+ax+b=-x^{2}+bx+a$，$\therefore2x^{2}+(a - b)x + b - a = 0$，$\therefore\Delta=(a - b)^{2}-8(b - a)=(a - b)^{2}+8(a - b)$.
$\because a＞b$，$\therefore\Delta=(a - b)^{2}+8(a - b)＞0$，$\therefore$函数$y_{1}$和$y_{2}$的图象有两个交点，故A正确；
对于B，$\because$函数$y_{1}$和$y_{2}$的值互为相反数，$\therefore x^{2}+ax+b+(-x^{2}+bx+a)=0$，$\therefore(a + b)x+(a + b)=0$，$\therefore(a + b)(x + 1)=0$，$\therefore a + b = 0$或$x + 1 = 0$，故B错误；
对于C，令$y_{1}=y_{2}$，$\therefore x^{2}+ax+b=-x^{2}+bx+a$，$\therefore2x^{2}+(a - b)x + b - a = 0$.
又$\because$当$x = 1$时，$2 + a - b + b - a = 2\neq0$，$\therefore$当$x = 1$时，函数$y_{1}$和$y_{2}$的值不相等，故C错误；
对于D，令$y_{1}=y_{2}$，$\therefore x^{2}+ax+b=-x^{2}+bx+a$，$\therefore$结合A可得，两个图象有两个公共点，且不能确定是不是定点，故D错误.故选：A.

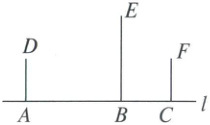
10. 如图，点 $ A $，$ B $，$ C $ 在直线 $ l $ 上，$ AD \perp l $，$ AD // BE // CF $，且过点 $ D $，$ E $，$ F $ 三点的圆的圆心在直线 $ l $ 上。若 $ AD = CF = 1 $，$ BE = 2 $，则 $ AB · BC $ 的值是（ ）

A.3
B.4
C.5
D.6

答案：
10.A 解析：方法一 如图1，连结$DF$交$BE$于点$M$，延长$EB$交圆于点$N$，连结$DE$，$FN$，

$\because\overset\frown{EF}=\overset\frown{EF}$，$\therefore\angle EDM=\angle FNM$.
$\because\angle EMD=\angle FMN$，$\therefore\triangle DEM\backsim\triangle NFM$，$\therefore\frac{DM}{MN}=\frac{EM}{FM}$，$\therefore DM· FM=EM· MN$.
$\because AD=CF=1$，$AD// CF$，$\therefore$四边形$ADFC$是平行四边形.
$\because AD\perp l$，$\therefore\angle DAC=90^{\circ}$，$\therefore$四边形$ADFC$是矩形，$\because BE// AD$，$\therefore BM=AD=CF=1$，$DM=AB$，$FM=BC$.
$\because BE=2$，$\therefore EM=BE - BM = 1$，由垂径定理可知$BN=BE=2$，$\therefore MN=BM + BN = 3$，$\therefore AB· BC=DM· FM=EM· MN=1×3=3$.故选A.
方法二 如图2，设圆心为$O$，连结$OD$，$OE$，$OF$，

$\because AD=CF$，$OD=OF$，$\therefore Rt\triangle OAD\cong Rt\triangle OCF(HL)$，$\therefore OA=OC$.
则$AB· BC=(OA + OB)(OC - OB)=(OA + OB)(OA - OB)=OA^{2}-OB^{2}=(OD^{2}-AD^{2})-(OE^{2}-BE^{2})=BE^{2}-AD^{2}=4 - 1 = 3$.故选：A.

11. 若 $ a : b = 3 : 1 $，则 $ a : (a + b) = $________。

答案： 11.$3:4$ 解析：$\because a:b=3:1$，$\therefore a=3b$，$\therefore a:(a + b)=3b:(3b + b)=3:4$.故答案为$3:4$.

12. 以 $ Rt \triangle ABC $ 的直角边 $ AB $ 为直径作圆，点 $ C $ 在________（填“圆内”“圆上”或“圆外”中的一个）。

答案： 12.圆外 解析：以$Rt\triangle ABC$的直角边$AB$为直径作圆，设圆心为$O$，$\therefore$点$C$，$O$与$Rt\triangle ABC$的直角顶点构成直角三角形，$OC$为直角三角形的斜边，$\therefore OC＞$所构成直角三角形的直角边，即$OC＞\frac{1}{2}AB$，$\therefore d＞r$，$\therefore$点$C$在圆外.故答案为圆外.

13. 在平面直角坐标系中，函数 $ y = -x^2 - x - 1 $ 的图象开口向________。

答案： 13.下 解析：由二次项系数$a=-1$，得函数$y=-x^{2}-x - 1$的图象开口向下.故答案为下.

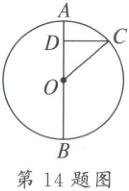
14. 如图，已知 $ AB $ 是 $ \odot O $ 的直径，点 $ C $ 在圆上，$ CD \perp AB $，与半径 $ OA $ 交于点 $ D $。若 $ OD = 2AD $，则 $ \sin \angle COD = $________。

答案： 14.$\frac{\sqrt{5}}{3}$ 解析：设$AD=x$，$\therefore OD=2AD=2x$，$OC=OA=3x$，$\because CD\perp AB$，$\therefore\angle ODC=90^{\circ}$，$\therefore CD=\sqrt{OC^{2}-OD^{2}}=\sqrt{5}x$，$\therefore\sin\angle COD=\frac{CD}{OC}=\frac{\sqrt{5}x}{3x}=\frac{\sqrt{5}}{3}$.故答案为$\frac{\sqrt{5}}{3}$.

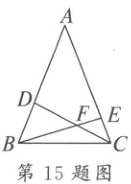
15. 如图，在 $ \triangle ABC $ 中，$ AB = AC $，点 $ D $，$ E $ 分别在 $ AB $，$ AC $ 上，$ AD ＜ AE $，连结 $ CD $，$ BE $，交于点 $ F $。若 $ CD = BE $，则图中与 $ \triangle ABE $ 相似的三角形是________。

答案：
15.$\triangle FBD$ 解析：如图，在$AC$上截取$CG=BD$，
$\because AB=AC$，$\therefore\angle DBC=\angle GCB$，

$\because BC=CB$，$\therefore\triangle DBC\cong\triangle GCB(SAS)$，$\therefore BG=CD$，$\angle BDF=\angle BGE$.
$\because CD=BE$，$\therefore BG=BE$，$\therefore\angle BGE=\angle BEG$，$\therefore\angle BDF=\angle BEA$.
$\because\angle DBF=\angle ABE$，$\therefore\triangle ABE\backsim\triangle FBD$，$\therefore$图中与$\triangle ABE$相似的三角形是$\triangle FBD$.故答案为$\triangle FBD$.

16. 在平面直角坐标系中，二次函数 $ y = 2x^2 - 4x + c $ 的图象过点 $ A(2, y_1) $，$ B(-2, y_2) $，$ C(m, n) $。若 $ y_1 ＜ n ＜ y_2 $，则 $ m $ 的取值范围是________。

答案： 16.$-2＜m＜0$或$2＜m＜4$ 解析：$\because$二次函数$y=2x^{2}-4x + c=2(x - 1)^{2}+c - 2$，$\therefore$抛物线开口向上，对称轴为直线$x = 1$，
$\because$二次函数$y=2x^{2}-4x + c$的图象过点$A(2,y_{1})$，$B(-2,y_{2})$，$C(m,n)$，$\therefore$点$C(m,n)$关于直线$x = 1$的对称点$(2 - m,n)$在二次函数$y=2x^{2}-4x + c$的图象上.
$\because y_{1}＜n＜y_{2}$，$\therefore$当$m＜1$时，则$\begin{cases}m＞-2\\2 - m＞2\end{cases}$，解得$-2＜m＜0$；当$m＞1$时，则$\begin{cases}m＞2\\2 - m＞-2\end{cases}$，解得$2＜m＜4$，综上，$m$的取值范围是$-2＜m＜0$或$2＜m＜4$.故答案为$-2＜m＜0$或$2＜m＜4$.

17. （8分）（1）计算：$ \sin 45° - \cos 45° - \tan 60° $；
（2）二次函数 $ y = x^2 + bx + c $，当 $ x = 0 $ 时，$ y = 0 $；当 $ x = 2 $ 时，$ y = 2 $，求 $ b $ 和 $ c $ 的值。

答案： 17.解：
(1)原式=$\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}-\sqrt{3}=-\sqrt{3}$.
(2)把$x = 0$，$y = 0$；$x = 2$，$y = 2$分别代入$y=x^{2}+bx+c$，得$\begin{cases}c=0\\4 + 2b + c = 2\end{cases}$，解得$\begin{cases}b=-1\\c=0\end{cases}$，即$b$的值为$-1$，$c$的值为$0$.