《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

1. 下列图形中，不能由一个图形通过旋转而成的为(C)

答案：
1.C　解析:不能由一个图形通过旋转而成的为是
　　　　　　　　　　
　故选C.

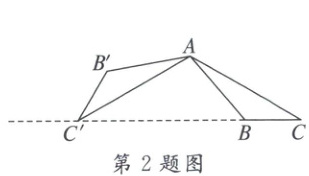
2. 如图，将△ABC绕点A顺时针旋转120°得到△AB'C'，若点C，B，C'共线，则∠ACB的度数为(C)

A.60°
B.45°
C.30°
D.15°

答案： 2.C　解析:
∵将△ABC绕点A顺时针旋转120°得到△AB'C',且点C,B,C'共线，
∴AC=AC’,∠CAC'=120°,
∴∠ACB=∠AC'C=$\frac{1}{2}$(180°−120°)=30°.
故选C.

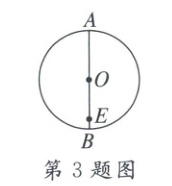
3. 如图，⊙O的直径AB=10，E在⊙O内，且OE=4，则过点E的所有弦中，最短弦为(B)

A.4
B.6
C.8
D.10

答案：
3.B　解析:如图,OC=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5,
　　　　　　　　　　　　　　　　　　　　 在Rt△OEC中,CE=$\sqrt{OC^{2}-OE^{2}}$=$\sqrt{5^{2}-4^{2}}$=3.
∵OE⊥CD,OE过圆心O,
∴CD=2CE=6,
　即最短弦是6.
　故选B.

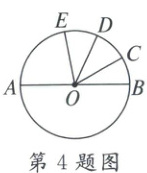
4. 如图，AB是⊙O的直径，$\overset{\frown}{BC}=\overset{\frown}{CD}=\overset{\frown}{DE}$，若∠COD=35°，则∠AOE的度数是(C)

A.35°
B.55°
C.75°
D.95°

答案： 4.C　解析:
∵$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$，∠COD=35°,
∴∠BOC=∠EOD=∠COD=35°,
∴∠AOE=180°−∠EOD−∠COD−∠BOC=75°.
　故选C.

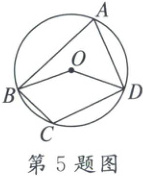
5. 如图，⊙O是四边形ABCD的外接圆，连结OB，OD，若∠BCD=110°，则∠BOD的大小为(D)

A.110°
B.120°
C.130°
D.140°

答案： 5.D　解析:
∵四边形ABCD内接于⊙O,∠BCD=110°,
∴∠A=180°−∠BCD=70°,
　由圆周角定理得，∠BOD=2∠A=140°.
　故选D.

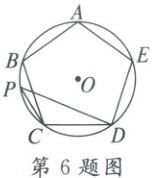
6. 如图，正五边形ABCDE内接于⊙O，点P是劣弧BC上一点(点P不与点C重合)，则∠CPD=(B)

A.45°
B.36°
C.35°
D.30°

答案：
6.B　解析:如图，连结OC,OD，
∵多边形ABCDE是正五边形，
∴∠COD=$\frac{360°}{5}$=72°,
∴∠CPD=$\frac{1}{2}$∠COD=36°.
　故选B.
　　　　　　　　　

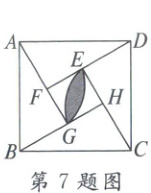
7. 在如图所示的“赵爽弦图”中，它是由四个全等的直角三角形与中间的小正方形EFGH拼成的大正方形ABCD，分别以点F，H为圆心，EF长为半径作弧，若AB=5，E为DF的中点，则图中阴影部分的面积为(A)

A.$\frac{5}{2}\pi - 5$
B.$\frac{5}{2}\pi - \frac{5}{2}$
C.$5\pi - 5$
D.$5\pi - 10$

答案： 7.A　解析:
∵△AFD≌△DEC,
∴AF=DE,
∵E为DF的中点，
∴EF=DE=AF,
∵四边形ABCD是正方形，
∴AD=AB=5,
　设EF=DE=AF=x,
　在Rt△AFD中,$AD^{2}=AF^{2}+DF^{2}$，
∴$5^{2}=x^{2}+(2x)^{2}$，
∴$x=\sqrt{5}$(负值已舍去)，
　即$EF=\sqrt{5}$，
∴$S_{阴影部分}=S_{扇形FEG}+S_{扇形HEG}-S_{正方形EFGH}$
　=$\frac{90\pi×(\sqrt{5})^{2}}{360}+\frac{90\pi×(\sqrt{5})^{2}}{360}-(\sqrt{5})^{2}$
=$\frac{5\pi}{2}$−5.
　故选A.