《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

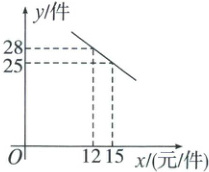
21. 毛泽东故居景区有一商店销售一种纪念品，这种纪念品的成本价为$10$元/件，已知销售价不低于成本价，且物价部门规定这种纪念品的销售价不高于$30$元/件，市场调查发现，该纪念品每天的销售量$y$（件）与销售价$x$（元/件）之间的函数关系如图所示。
（1）求$y$与$x$之间的函数表达式，并写出自变量$x$的取值范围；
（2）求每天的销售利润$W$（元）与销售价$x$（元/件）之间的函数表达式，并求出每件销售价为多少元时，每天的销售利润最大？最大利润是多少？

答案： 21.解:
(1)设y与x的函数表达式为y=kx+b，
　将(12,28),(15,25)代入，得
　　$\begin{cases}12k + b = 28\\15k + b = 25\end{cases}$
　解得$\begin{cases}k = -1\\b = 40\end{cases}$
　所以y与x的函数表达式为y=−x+40(10≤x≤30).
(2)根据题意知,W=(x−10)y
　　=(x−10)(−x+40)
　　=−x²+50x−400
　　=−(x−25)²+225,
∵a=−1＜0,10≤x≤30,
∴当x=25时，W取得最大值，最大值为225.
答:每件销售价为25元时，每天的销售利润最大，最大利润是225元

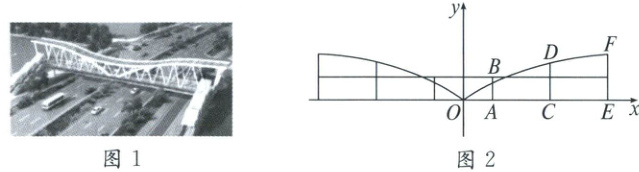
22. 图1是城市人行天桥的效果图，天桥顶部由四段完全相同的抛物线形钢架构成。可以把天桥单侧的两段钢架抽象成如图2所示两段抛物线，并建立如图所示的平面直角坐标系。已知天桥总长$50$米，并在人行道两侧各均匀分布着$6$根钢柱，其中$AB=3$米，$EF=5$米。
（1）如果抛物线经过原点$O$，顶点刚好落在点$F$，求该抛物线的表达式；
（2）在（1）的条件下求单侧$6$根钢柱的总长度；
（3）现需要修改钢架结构，将抛物线顶点移到$EF$右侧，到$EF$水平距离为$1$米，且使抛物线经过点$F$，与钢柱$AB$有交点，求此时顶点的纵坐标$k$的取值范围。

答案： 22.解:
(1)由题意可得顶点F的坐标是(25,5)，
　　设抛物线表达式为y=a(x−25)²+5，
∵抛物线经过原点(0,0)，
∴将(0,0)代入,得a(0−25)²+5=0,
　　解得a=−$\frac{1}{125}$,
∴该抛物线的表达式为y=−$\frac{1}{125}$(x−25)²+5.
(2)由题意可得，OC=15米，
　　将x=15代入y=−$\frac{1}{125}$(x−25)²+5,
　　解得y=$\frac{21}{5}$,
∴CD=$\frac{21}{5}$米，
∴2(AB+CD+EF)=2×(3+$\frac{21}{5}$+5)=$\frac{122}{5}$(米)，
∴6根钢柱的总长度为$\frac{122}{5}$米.
(3)由题意，得修改钢架结构后抛物线顶点坐标为(26,k),
∴设抛物线表达式为y=a'(x−26)²+k.
∵抛物线经过点F(25,5)，
∴5=a'(25−26)²+k,
∴a'=−k+5,
　　当x=5时,y=a'(5−26)²+k=441a'+k,
∵抛物线与钢柱AB有交点，
∴0≤441a'+k≤3,
　　将a'=−k+5代入,可得0≤441(−k+5)+k≤3,
∴−2205≤−440k≤−2202,
　　解得$\frac{1101}{220}$≤k≤$\frac{441}{88}$.
∴顶点的纵坐标k的取值范围为$\frac{1101}{220}$≤k≤$\frac{441}{88}$.