第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
18. (6分)某校推荐了4名学生作为区域中学生中华经典诵读比赛主持人,其中1名七年级女生、2名八年级学生(刚好1名男生和1名女生)、1名九年级男生。
(1)若从4名学生中任选一名作为主持人,抽到九年级学生的概率是
(2)若先从八年级的2名学生中任抽1名,再从剩下的3名学生任抽1名,求恰好抽到一名男生和一名女生的概率,请用列表格或画树状图等方法说明。
(1)若从4名学生中任选一名作为主持人,抽到九年级学生的概率是
$\frac{1}{4}$
;(2)若先从八年级的2名学生中任抽1名,再从剩下的3名学生任抽1名,求恰好抽到一名男生和一名女生的概率,请用列表格或画树状图等方法说明。
答案:
18.解:
(1)$\frac{1}{4}$
(2)列表如下:
| | 七年级 | 八年级 | 八年级 | 九年级 |
| --- | --- | --- | --- | --- |
| | 女生 | 男生 | 女生 | 男生 |
| 八年级男生 | (男,女) | | (男,女) | (男,男) |
| 八年级女生 | (女,女) | (女,男) | | (女,男) |
所有等可能的结果共有$6$种,按要求恰好抽到一名男生和一名女生(记为事件$B$)的情况只有$4$种,所以$P(B) = \frac{4}{6}=\frac{2}{3}$.
(1)$\frac{1}{4}$
(2)列表如下:
| | 七年级 | 八年级 | 八年级 | 九年级 |
| --- | --- | --- | --- | --- |
| | 女生 | 男生 | 女生 | 男生 |
| 八年级男生 | (男,女) | | (男,女) | (男,男) |
| 八年级女生 | (女,女) | (女,男) | | (女,男) |
所有等可能的结果共有$6$种,按要求恰好抽到一名男生和一名女生(记为事件$B$)的情况只有$4$种,所以$P(B) = \frac{4}{6}=\frac{2}{3}$.
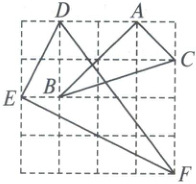
19. (6分)如图$4×4$正方形方格中的两个$\triangle ABC$和$\triangle DEF$的顶点都是格点。
(1)求证:$\triangle ABC\sim\triangle EFD$;
(2)在该网格中画一个顶点都是格点的三角形,要求与$\triangle ABC$相似且面积最小。
(1)求证:$\triangle ABC\sim\triangle EFD$;
(2)在该网格中画一个顶点都是格点的三角形,要求与$\triangle ABC$相似且面积最小。

答案:
19.
(1)证明:$4 × 4$正方形方格中的两个$\triangle ABC$和$\triangle DEF$的顶点都是格点.设网格中每个小正方形的边长为$1$,
∴$AC = \sqrt{2}$,$AB = 2\sqrt{2}$,$BC = \sqrt{10}$,$DE = \sqrt{5}$,$EF = 2\sqrt{5}$,
$DF = 5$,
∴$\frac{AC}{DE}=\frac{AB}{EF}=\frac{BC}{DF}=\frac{\sqrt{10}}{5}$,
∴$\triangle ABC \backsim \triangle EFD$.
(2)解:如图,$\triangle PQR$就是所求的三角形.(答案不唯一)

19.
(1)证明:$4 × 4$正方形方格中的两个$\triangle ABC$和$\triangle DEF$的顶点都是格点.设网格中每个小正方形的边长为$1$,
∴$AC = \sqrt{2}$,$AB = 2\sqrt{2}$,$BC = \sqrt{10}$,$DE = \sqrt{5}$,$EF = 2\sqrt{5}$,
$DF = 5$,
∴$\frac{AC}{DE}=\frac{AB}{EF}=\frac{BC}{DF}=\frac{\sqrt{10}}{5}$,
∴$\triangle ABC \backsim \triangle EFD$.
(2)解:如图,$\triangle PQR$就是所求的三角形.(答案不唯一)

查看更多完整答案,请扫码查看


