《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

8. 在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$AB = 13$，$AC = 12$，则$\cos A =$$\frac{12}{13}$。

答案： 8.$\frac{12}{13}$　解析:在$Rt\triangle ABC$中$,\angle C = 90°$，
　$AB = 13,AC = 12$，
　$\therefore \cos A = \frac{AC}{AB} = \frac{12}{13}$.

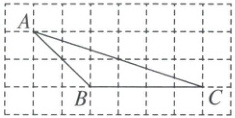
9. 如图，在$8× 4$的矩形网格中，每个小正方形的边长都是1，若$\triangle ABC$的三个顶点在图中相应的格点上，则$\tan \angle ACB$的值为$\frac{1}{3}$。

答案： 9.$\frac{1}{3}$　解析:由图形知:$\tan\angle ACB = \frac{2}{6} = \frac{1}{3}$.

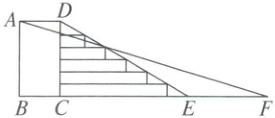
10. 为了学生的安全，某校决定把一段如图所示的步梯路段进行改造。已知四边形$ABCD$为矩形，$DE = 10m$，其坡度为$i_1 = 1 : \sqrt{3}$，将步梯$DE$改造为斜坡$AF$，其坡度为$i_2 = 1 : 4$，则斜坡$AF$的长度是20.62m。(结果精确到$0.01m$，参考数据：$\sqrt{3} \approx 1.732$，$\sqrt{17} \approx 4.123$)

答案： 10.20.62　解析:$\because$斜坡$DE$的坡度为$i_1 = 1 : \sqrt{3}$，
　$\therefore \tan\angle DEC = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}$，
　$\therefore \angle DEC = 30°$，
　$\therefore DC = \frac{1}{2}DE = 5$（m），
　$\because$四边形$ABCD$为矩形，
　$\therefore AB = CD = 5$m，
　$\because$斜坡$AF$的坡度为$i_2 = 1 : 4,AB = 5$m，
　$\therefore BF = 4AB = 20$（m），
　在$Rt\triangle ABF$中$,AF = \sqrt{AB^2 + BF^2} = \sqrt{5^2 + 20^2} \approx 20.62$（m），
　$\therefore$斜坡$AF$的长度约为$20.62$m.

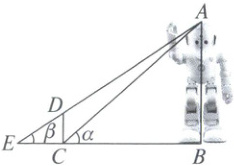
11. 某商场引进消毒机器人每天进行全场消毒工作，该机器人采取精准直线喷射技术，实现了准确、快速和节约的目标。在设置参数的时候，工作人员通过对商场门口身形高大的“大黄蜂”进行多次消毒试验发现：如图，若对$A$点进行消毒，适当调整机器人$CD$到$AB$的距离，使得$\sin (\alpha - \beta)$的值尽可能的大，能提高消毒的效率。已知“大黄蜂”$AB$身高2.5米，机器人$CD$高0.4米。则当$\sin (\alpha - \beta)$最大时，机器人$CD$和“大黄蜂”$AB$之间距离$BC$等于$\frac{\sqrt{21}}{2}$m。

答案：
11.$\frac{\sqrt{21}}{2}$　解析:如图，过点$C$作$CF \perp AE$于点$F$，
　　　　　　　　
　设$BC = x$m，
　根据题意得$CD \perp BE,AB \perp BE,AB = 2.5$m,$CD = 0.4$m，
　$\therefore CD // AB$，
　$\therefore \triangle CDE \backsim \triangle BAE$，
　$\therefore \frac{CD}{AB} = \frac{CE}{BE}$，即$\frac{0.4}{2.5} = \frac{CE}{CE + x}$，
　解得$CE = \frac{4}{21}x$m，
　$\because \alpha = \beta + \angle CAF$，
　$\therefore \angle CAF = \alpha - \beta$，
　$\therefore$当$\sin(\alpha - \beta)$最大时$,\sin\angle CAF$最大，
　$\therefore (\sin\angle CAF)^2$最大，即$\frac{CF^2}{AC^2}$最大，
　在$Rt\triangle ABC$中$,AC^2 = BC^2 + AB^2 = x^2 + \frac{25}{4} = \frac{4x^2 + 25}{4}$，
　在$Rt\triangle CDE$中$,DE^2 = CE^2 + CD^2 = \frac{16}{441}x^2 + \frac{4}{25}$，
　$\because \frac{1}{2}CD · CE = \frac{1}{2}DE · CF$，
　$\therefore CD^2 · CE^2 = DE^2 · CF^2$，
　$\therefore CF^2 = \frac{CD^2 · CE^2}{DE^2} = \frac{\frac{4}{25} × \frac{16}{441}x^2}{\frac{16}{441}x^2 + \frac{4}{25}} = \frac{16x^2}{441 + 100x^2}$，
　$\therefore \frac{CF^2}{AC^2} = \frac{\frac{16x^2}{441 + 100x^2}}{\frac{4x^2 + 25}{4}} = \frac{64x^2}{400x^4 + 4264x^2 + 11025}$，
　$\because x \neq 0$，
　$\therefore \frac{CF^2}{AC^2} = \frac{64}{400x^2 + \frac{11025}{x^2} + 4264}$，
　$\because \frac{CF^2}{AC^2}$最大，
　$\therefore 400x^2 + \frac{11025}{x^2} + 4264$最小，即$400x^2 + \frac{11025}{x^2}$最小，
　$\because \left( \sqrt{400x^2} - \sqrt{\frac{11025}{x^2}} \right)^2 \geq 0$，即$400x^2 + \frac{11025}{x^2} \geq 2\sqrt{400x^2 · \frac{11025}{x^2}}$，
　$\therefore$当$\sqrt{400x^2} = \sqrt{\frac{11025}{x^2}}$，即$x = \frac{\sqrt{21}}{2}$或$-\frac{\sqrt{21}}{2}$（舍去）时，$400x^2 + \frac{11025}{x^2}$最小，
　即当$\sin(\alpha - \beta)$最大时，机器人$CD$和“大黄蜂”$AB$之间距离$BC$为$\frac{\sqrt{21}}{2}$m.