《2025年领智优选浙江期末复习卷九年级数学全一册浙教版》

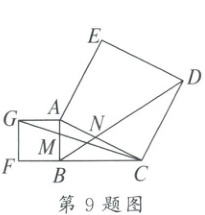
9. 如图，在 $Rt\triangle ABC$ 中，$\angle ABC = 90^{\circ}$，以 $AB$，$AC$ 为边分别向外作正方形 $ABFG$ 和正方形 $ACDE$，$CG$ 交 $AB$ 于点 $M$，$BD$ 交 $AC$ 于点 $N$。若 $\frac{GM}{CM} = \frac{1}{2}$，则 $\frac{AN}{CN} =$(B)

A.$\frac{1}{2}$
B.$\frac{3}{4}$
C.$\frac{2\sqrt{5}}{5}$
D.1

答案：
9.B 解析：如图，过点D作$DP\perp BC$，交AC的延长线于点P，交BC的延长线于点H。$\because AG// BF$，$\therefore \triangle AGM\sim \triangle BCM$，$\therefore \frac{AG}{BC} = \frac{GM}{CM} = \frac{1}{2}$，$\therefore$设$AG = a = AB$，则$BC = 2a$。$\because DH\perp BC$，$AB\perp BC$，$\therefore \angle DHC = \angle ABC = \angle ACD = 90°$，$AB// DH$，$\therefore \angle DCH + \angle ACB = 90° = \angle ACB + \angle BAC$，$\therefore \angle DCH = \angle BAC$。在$\triangle ABC$和$\triangle CHD$中，$\begin{cases} \angle ABC = \angle CHD \\ \angle BAC = \angle HCD \\ AC = CD \end{cases}$，$\therefore \triangle ABC\cong \triangle CHD(AAS)$，$\therefore CH = AB = a$，$DH = CB = 2a$。$\because AB// DP$，$\therefore \triangle ABC\sim \triangle PHC$，$\therefore \frac{AC}{PC} = \frac{AB}{PH} = \frac{BC}{HC} = 2$，$\therefore HP = \frac{1}{2}AB = \frac{a}{2}$，$AC = 2CP$，$\therefore DP = \frac{5}{2}a$。$\because AB// DH$，$\therefore \triangle ABN\sim \triangle PDN$，$\therefore \frac{AN}{PN} = \frac{AB}{PD} = \frac{2}{5}$，设$AN = 2b$，则$NP = 5b$，$\therefore AP = 7b = AC + CP = 3CP$，$\therefore CP = \frac{7b}{3}$，$\therefore AC = \frac{14b}{3}$，$CN = \frac{8b}{3}$，$\therefore \frac{AN}{CN} = \frac{2b}{\frac{8b}{3}} = \frac{3}{4}$。故选：B。

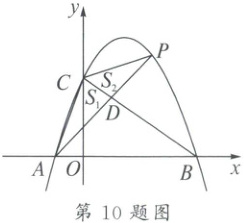
10. 如图，在平面直角坐标系中 $y = -\frac{3}{4}(x - 4)(x + 1)$，与 $x$ 轴交于 $A$，$B$ 两点(点 $A$ 在点 $B$ 的左侧)，与 $y$ 轴交于点 $C$，点 $P$ 是 $BC$ 上方抛物线上一点，连结 $AP$ 交 $BC$ 于 $D$，连结 $AC$，$CP$，记 $\triangle ACD$ 的面积为 $S_1$，$\triangle PCD$ 的面积为 $S_2$，则 $\frac{S_2}{S_1}$ 的最大值为(C)

A.$\frac{3}{4}$
B.$\frac{3}{5}$
C.$\frac{4}{5}$
D.1

答案：
10.C 解析：由题意知$\frac{S_2}{S_1} = \frac{PD}{AD}$，如图，过点P作x轴的平行线交BC的延长线于点M。

$\because PM// x$轴，$\therefore \triangle PMD\sim \triangle ABD$，$\therefore \frac{PD}{AD} = \frac{PM}{AB}$。由$y = -\frac{3}{4}(x - 4)(x + 1)$，得$A(-1,0)$，$B(4,0)$，$\therefore AB = 4 - (-1) = 5$。将$x = 0$代入$y = -\frac{3}{4}(x - 4)(x + 1)$，得$y = 3$，$\therefore$点C的坐标为$(0,3)$。设直线BC的函数表达式为$y = kx + b(k\neq0)$，则$\begin{cases} 4k + b = 0 \\ b = 3 \end{cases}$，解得$\begin{cases} k = -\frac{3}{4} \\ b = 3 \end{cases}$，$\therefore$直线BC的函数表达式为$y = -\frac{3}{4}x + 3$。$\because y = -\frac{3}{4}(x - 4)(x + 1) = -\frac{3}{4}x^2 + \frac{9}{4}x + 3$，令点P坐标为$(m,-\frac{3}{4}m^2 + \frac{9}{4}m + 3)$，则$y_M = -\frac{3}{4}m^2 + \frac{9}{4}m + 3$，$\therefore -\frac{3}{4}m^2 + \frac{9}{4}m + 3 = -\frac{3}{4}x_M + 3$，$\therefore x_M = m^2 - 3m$，则$PM = m - (m^2 - 3m) = -m^2 + 4m$，$\therefore \frac{PM}{AB} = \frac{-m^2 + 4m}{5} = -\frac{1}{5}(m - 2)^2 + \frac{4}{5}$，则当$m = 2$时，$\frac{PM}{AB}$有最大值为$\frac{4}{5}$，即$\frac{S_2}{S_1}$的最大值为$\frac{4}{5}$。故选：C。

11. 抛物线 $y = -2(x - 3)^2 + 8$ 的顶点坐标是(3,8) 。

答案： 11.$(3,8)$ 解析：$\because$抛物线为$y = -2(x - 3)^2 + 8$，$\therefore$抛物线的顶点坐标为$(3,8)$。故答案为$(3,8)$。

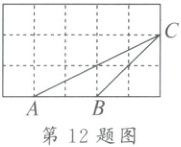
12. 如图，$\triangle ABC$ 的顶点都在方格纸的格点上，则 $\tan A =$$\frac{1}{2}$ 。

答案：
12.$\frac{1}{2}$ 解析：如图，在$\triangle ACD$中，$\because \angle ADC = 90°$，$CD = 2$，$AD = 4$，$\therefore \tan A = \frac{CD}{AD} = \frac{2}{4} = \frac{1}{2}$。故答案为$\frac{1}{2}$。

13. 已知点 $P$ 是线段 $AB$ 的黄金分割点（$AP ＞ PB$），$AB = 6$，那么 $AP$ 的长是$3\sqrt{5}-3$ 。

答案： 13.$3\sqrt{5} - 3$ 解析：由于P为线段$AB = 6$的黄金分割点，且AP是较长线段，则$AP = 6× \frac{\sqrt{5} - 1}{2} = 3\sqrt{5} - 3$。故答案为$3\sqrt{5} - 3$。

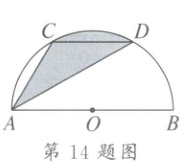
14. 如图，$C$，$D$ 是以 $AB$ 为直径的半圆周的三等分点，$CD = 6\ cm$，则阴影部分的面积是$6\pi$ $cm^2$。（结果保留 $\pi$）

答案：
14.$6\pi$ 解析：如图，连结OC，OD，$\because$C，D是以AB为直径的半圆周的三等分点，$\therefore \angle AOC = \angle COD = \angle BOD = 60°$。又$\because OC = OD$，$\therefore \triangle OCD$是等边三角形，$\therefore \angle CDO = 60°$，$OD = CD = 6cm$，$\therefore \angle CDO = \angle BOD$，$\therefore CD// AB$，$\therefore S_{\triangle OCD} = S_{\triangle ACD}$，$\therefore S_{阴影} = S_{扇形OCD}$。又$\because S_{扇形OCD} = \frac{60× \pi× 6^2}{360} = 6\pi(cm^2)$，$\therefore S_{阴影} = 6\picm^2$。故答案为$6\pi$。

15. 已知抛物线 $y = a(x - h)^2 + k$ 与直线 $y = 1$ 有两个交点 $A(-1,1)$，$B(3,1)$，抛物线 $y = a(x - h + m)^2 + k$ 与直线 $y = 1$ 的一个交点是 $(-3,1)$，则 $m$ 的值是2或6 。

答案： 15.2或6 解析：由抛物线$y = a(x - h)^2 + k$向左平移m个单位得到抛物线$y = a(x - h + m)^2 + k$，而$A(-1,1)$，$B(3,1)$向左平移2或6个单位得到点$(-3,1)$，得$m = 2$或6。故答案为2或6。

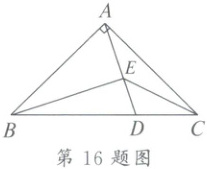
16. 如图，在等腰 $Rt\triangle ABC$ 中，$\angle BAC = 90^{\circ}$，$D$ 是 $BC$ 边上一点，$BD = 2DC$，连结 $AD$，点 $E$ 在线段 $AD$ 上，若 $\angle BEC = 135^{\circ}$，则 $\frac{CE}{AC}$ 的值为$\frac{\sqrt{10}}{5}$ 。

答案：
16.$\frac{\sqrt{10}}{5}$ 解析：如图，过点E作$PQ// BC$交AB于点P，交AC于点Q，则$\triangle APE\sim \triangle ABD$，$\triangle AQE\sim \triangle ACD$，$\therefore \frac{PE}{BD} = \frac{AE}{AD} = \frac{EQ}{DC}$。$\because BD = 2DC$，$\therefore \frac{PE}{2DC} = \frac{EQ}{DC}$，$\therefore \frac{PE}{EQ} = \frac{2DC}{DC} = 2$，$\therefore PE = 2EQ = PQ - EQ$，$\therefore EQ = \frac{1}{3}PQ$。$\because \triangle ABC$是等腰直角三角形，$\angle BAC = 90°$，$\therefore AB = AC$，$\angle ABC = \angle ACB = 45°$，$\therefore \angle BPE = \angle EQC = 135°$，$\angle APQ = \angle AQP$，$\therefore AP = AQ$，$\therefore BP = AB - AP = AC - AQ = QC$。$\because \angle BEC = 135°$，$\therefore \angle QEC + \angle PEB = 45°$，$\therefore \angle PBE + \angle PEB = \angle APQ = 45°$，$\therefore \angle PBE = \angle QEC$，$\therefore \triangle PBE\sim \triangle QEC$，$\therefore \frac{BP}{EQ} = \frac{PE}{QC}$，$\therefore QC^2 = 2EQ^2$，$\therefore QC = \sqrt{2}EQ = \sqrt{2}× \frac{1}{3}PQ = \frac{\sqrt{2}}{3}PQ$。$\because PQ = \sqrt{AP^2 + AQ^2} = \sqrt{2}AQ$，$EQ = \frac{\sqrt{2}}{2}QC$，$\therefore QC = \frac{\sqrt{2}}{3}× \sqrt{2}AQ = \frac{2}{3}AQ = \frac{2}{3}(AC - QC)$，$\therefore QC = \frac{2}{5}AC$，$\therefore EQ = \frac{\sqrt{2}}{2}× \frac{2}{5}AC = \frac{\sqrt{2}}{5}AC$。$\because \angle CQE = \angle BEC = 135°$，$\angle CEQ = \angle BCE$，$\therefore \triangle CEQ\sim \triangle BCE$，$\therefore \frac{EQ}{CE} = \frac{CE}{BC}$，$\therefore CE^2 = EQ· BC = \frac{\sqrt{2}}{5}AC× \sqrt{2}AC = \frac{2}{5}AC^2$，$\therefore \frac{CE^2}{AC^2} = \frac{2}{5}$，$\therefore \frac{CE}{AC} = \frac{\sqrt{10}}{5}$。故答案为$\frac{\sqrt{10}}{5}$。

17. (8 分) 计算：
（1）$\cos 30^{\circ} · \tan 60^{\circ} - \sqrt{2} \sin 45^{\circ}$；
（2）已知 $x : y = 1 : 2$，求代数式 $\frac{3x - y}{x + 2y}$ 的值。

答案： 17.解：
(1)$\cos 30° · \tan 60° - \sqrt{2}\sin 45° = \frac{\sqrt{3}}{2}× \sqrt{3} - \sqrt{2}× \frac{\sqrt{2}}{2} = \frac{3}{2} - 1 = \frac{1}{2}$。
(2)$\because x:y = 1:2$，$\therefore y = 2x$，$\therefore \frac{3x - y}{x + 2y} = \frac{3x - 2x}{x + 4x} = \frac{1}{5}$。