《2025年金版学案同步优学智慧作业七年级数学上册人教版》

- 练习 3 下图是小明家的部分结构平面图(单位：m),他打算把图中卧室以外的部分都铺上地砖.

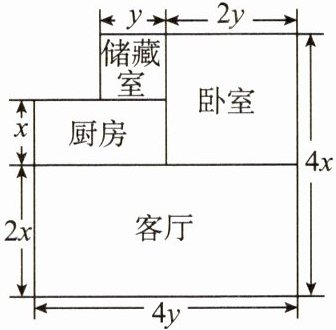
(1) 如果铺地砖的价格为 $60$ 元$/m^{2}$,那么铺地砖需要花多少元？
(2) 已知房屋的高为 $3$ m,现需要在客厅和卧室的墙壁上贴壁纸,那么需要多少平方米的壁纸(计算时不扣除门、窗所占的面积)?(假设 $x$,$y$ 表示的值为正整数)

答案：
(1)铺地砖的面积为(4x−2x−x)y+x(4y−2y)+2x·4y=xy+2xy+8xy=11xy(m²).铺地砖需要花60×11xy=660xy(元).答:铺地砖需要花660xy元.
(2)客厅和卧室的墙壁面积为3[2(2x+4y)+2(4x−2x+2y)]=3(4x+8y+8x−4x+4y)=12x+24y+12x+12y=(24x+36y)m².答:需要(24x+36y)m²的壁纸.

1. 下列式子去括号正确的是(D).
A.$(x^{2}+y)-2(x - y^{2})= x^{2}+y - 2x + y^{2}$
B.$a-(b - c)= a - b - c$
C.$-(a + b)-(-x + y)= -a + b + x - y$
D.$-3(x - y)+(a - b)= -3x + 3y + a - b$

答案： D

2. 化简：$(3a - b)-3(a + 3b)= ($B$)$.
A.$-2b$
B.$-10b$
C.$-2a - 10b$
D.$8b$

答案： B

3. 化简求值：$\frac{1}{2}x - 3(2x - \frac{2}{3}y^{2})+(-\frac{3}{2}x + y^{2})$,其中 $x = 1$,$y = 2$,则原式 $=$(5).
A.$6$
B.$-6$
C.$5$
D.$-5$

答案： C [解析]$\frac{1}{2}$x−3(2x−$\frac{2}{3}$y²)+(−$\frac{3}{2}$x+y²)=$\frac{1}{2}$x−6x+2y²−$\frac{3}{2}$x+y²=−7x+3y².当x=1，y=2时，原式=(−7)×1+3×2²=(−7)+12=5.故选C.

4. 某地区居民生活用水收费标准：每月用水量不超过 $20$ 立方米,每立方米 $a$ 元；超过部分每立方米 $(a + 1.2)$ 元. 该地区某用户上月用水量为 $25$ 立方米,则应缴水费为(A).
A.$(25a + 6)$ 元
B.$(25a + 30)$ 元
C.$25a$ 元
D.$(20a + 24)$ 元

答案： A [解析]由于某用户上月用水量为25立方米，超过20立方米，所以应缴水费为20a+(25−20)(a+1.2)=(25a+6)元.故选A.

5. 先化简,再求值：
$3a^{2}b - [2ab - 2(ab - \frac{3}{2}a^{2}b)+ab]$,其中 $a = -3$,$b = \frac{1}{3}$.

答案：

[解]原式$=3a^{2}b - (2ab - 2ab + 3a^{2}b + ab)$

$=3a^{2}b - 2ab + 2ab - 3a^{2}b - ab$

$=-ab$

当$a = -3$，$b = \frac{1}{3}$时，原式$=-(-3) × \frac{1}{3} = 1$