2025年金版学案同步优学智慧作业七年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金版学案同步优学智慧作业七年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
4. (跨学科融合)计算机老师设计了计算接力游戏,规则是每名同学只能利用前面一个同学的式子进一步计算,将计算的结果传给下一个同学,最后解决问题. 过程如下,下面(
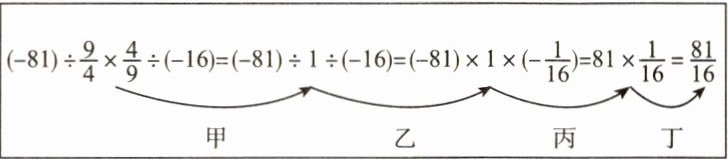
A.甲
B.乙
C.丙
D.丁
A
)同学负责的那一步出现了错误.
A.甲
B.乙
C.丙
D.丁
答案:
A
5. 先计算,再阅读材料,解决问题:
(1) 计算:$\left(\dfrac {1}{3}-\dfrac {1}{6}+\dfrac {1}{2}\right)× 12$;
(2) 认真阅读材料,解决问题:
计算:$\dfrac {1}{30}÷ \left(\dfrac {2}{3}-\dfrac {1}{10}+\dfrac {1}{6}-\dfrac {2}{5}\right)$.
分析:利用通分计算$\dfrac {2}{3}-\dfrac {1}{10}+\dfrac {1}{6}-\dfrac {2}{5}$的结果很麻烦,可以采用以下方法进行计算.
解:原式的倒数是:
$\begin{aligned}&\left(\dfrac {2}{3}-\dfrac {1}{10}+\dfrac {1}{6}-\dfrac {2}{5}\right)÷ \dfrac {1}{30}\\=&\left(\dfrac {2}{3}-\dfrac {1}{10}+\dfrac {1}{6}-\dfrac {2}{5}\right)× 30\\=&\dfrac {2}{3}× 30-\dfrac {1}{10}× 30+\dfrac {1}{6}× 30-\dfrac {2}{5}× 30\\=&20 - 3 + 5 - 12\\=&10.\end{aligned} $
故$\dfrac {1}{30}÷ \left(\dfrac {2}{3}-\dfrac {1}{10}+\dfrac {1}{6}-\dfrac {2}{5}\right)= \dfrac {1}{10}$.
请你根据对以上材料的理解,选择合适的方法计算:$\dfrac {1}{28}÷ \left(\dfrac {1}{4}-\dfrac {5}{14}-\dfrac {3}{7}\right)$.
(1)
(2)
(1) 计算:$\left(\dfrac {1}{3}-\dfrac {1}{6}+\dfrac {1}{2}\right)× 12$;
(2) 认真阅读材料,解决问题:
计算:$\dfrac {1}{30}÷ \left(\dfrac {2}{3}-\dfrac {1}{10}+\dfrac {1}{6}-\dfrac {2}{5}\right)$.
分析:利用通分计算$\dfrac {2}{3}-\dfrac {1}{10}+\dfrac {1}{6}-\dfrac {2}{5}$的结果很麻烦,可以采用以下方法进行计算.
解:原式的倒数是:
$\begin{aligned}&\left(\dfrac {2}{3}-\dfrac {1}{10}+\dfrac {1}{6}-\dfrac {2}{5}\right)÷ \dfrac {1}{30}\\=&\left(\dfrac {2}{3}-\dfrac {1}{10}+\dfrac {1}{6}-\dfrac {2}{5}\right)× 30\\=&\dfrac {2}{3}× 30-\dfrac {1}{10}× 30+\dfrac {1}{6}× 30-\dfrac {2}{5}× 30\\=&20 - 3 + 5 - 12\\=&10.\end{aligned} $
故$\dfrac {1}{30}÷ \left(\dfrac {2}{3}-\dfrac {1}{10}+\dfrac {1}{6}-\dfrac {2}{5}\right)= \dfrac {1}{10}$.
请你根据对以上材料的理解,选择合适的方法计算:$\dfrac {1}{28}÷ \left(\dfrac {1}{4}-\dfrac {5}{14}-\dfrac {3}{7}\right)$.
(1)
8
;(2)
$-\dfrac{1}{15}$
答案:
(1)$8$;
(2)$-\dfrac{1}{15}$
【解】
(1)原式$=\dfrac{1}{3}× 12-\dfrac{1}{6}× 12+\dfrac{1}{2}× 12=4-2+6=8$.
(2)原式的倒数是:
$\left(\dfrac{1}{4}-\dfrac{5}{14}-\dfrac{3}{7}\right)÷ \dfrac{1}{28}=\left(\dfrac{1}{4}-\dfrac{5}{14}-\dfrac{3}{7}\right)×28=\dfrac{1}{4}× 28-\dfrac{5}{14}× 28-\dfrac{3}{7}× 28=7-10-12=-15$.
故原式$=-\dfrac{1}{15}$.
(1)$8$;
(2)$-\dfrac{1}{15}$
【解】
(1)原式$=\dfrac{1}{3}× 12-\dfrac{1}{6}× 12+\dfrac{1}{2}× 12=4-2+6=8$.
(2)原式的倒数是:
$\left(\dfrac{1}{4}-\dfrac{5}{14}-\dfrac{3}{7}\right)÷ \dfrac{1}{28}=\left(\dfrac{1}{4}-\dfrac{5}{14}-\dfrac{3}{7}\right)×28=\dfrac{1}{4}× 28-\dfrac{5}{14}× 28-\dfrac{3}{7}× 28=7-10-12=-15$.
故原式$=-\dfrac{1}{15}$.
6. 对于$1 + 2× 3 - 4÷ 5$,不改变数字和运算符号的顺序,也不添加任何运算符号,对至少两个数添加括号后并计算出结果,称为一种“加括号操作”. 例如:$(1 + 2× 3)-4÷ 5= \dfrac {31}{5}$是一种“加括号操作”,$\dfrac {31}{5}$是其运算结果;$(1 + 2)× (3 - 4)÷ 5= -\dfrac {3}{5}$是一种“加括号操作”,$-\dfrac {3}{5}$是其运算结果. 给出下列说法:①至少存在一种“加括号操作”的运算结果是$\dfrac {7}{5}$;②不存在任何“加括号操作”的运算结果是$\dfrac {26}{5}$;③所有“加括号操作”共有$7$种不同的运算结果. 其中正确的个数是(
A.$0$
B.$1$
C.$2$
D.$3$
D
).A.$0$
B.$1$
C.$2$
D.$3$
答案:
D
【解析】对于$1 + 2× 3 - 4÷ 5$,进行“加括号操作”的所有结果如下:
$(1+2)× 3-4÷ 5=\dfrac{41}{5}$,$(1+2× 3)-4÷ 5=\dfrac{31}{5}$,$(1+2× 3-4)÷ 5=\dfrac{3}{5}$,$1+(2×3)-4÷ 5=\dfrac{31}{5}$,$1+(2× 3-4)÷ 5=\dfrac{7}{5}$,$1+(2× 3-4÷ 5)=\dfrac{31}{5}$,$1+2× (3-4)÷ 5=\dfrac{3}{5}$,$1+2× (3-4÷ 5)=\dfrac{27}{5}$,$1+2× 3-(4÷5)=\dfrac{31}{5}$,$(1+2)× (3-4)÷ 5=-\dfrac{3}{5}$,$(1+2)× (3-4÷ 5)=\dfrac{33}{5}$,$(1+2)× 3-(4÷ 5)=\dfrac{41}{5}$.
观察以上结果发现:至少存在一种“加括号操作”的运算结果是$\dfrac{7}{5}$,故①正确;不存在任何“加括号操作”的运算结果是$\dfrac{26}{5}$,故②正确;所有“加括号操作”共有7种不同的运算结果,即$\dfrac{41}{5}$,$\dfrac{31}{5}$,$\dfrac{3}{5}$,$\dfrac{7}{5}$,$\dfrac{27}{5}$,$-\dfrac{3}{5}$,$\dfrac{33}{5}$,故③正确.故选D.
【解析】对于$1 + 2× 3 - 4÷ 5$,进行“加括号操作”的所有结果如下:
$(1+2)× 3-4÷ 5=\dfrac{41}{5}$,$(1+2× 3)-4÷ 5=\dfrac{31}{5}$,$(1+2× 3-4)÷ 5=\dfrac{3}{5}$,$1+(2×3)-4÷ 5=\dfrac{31}{5}$,$1+(2× 3-4)÷ 5=\dfrac{7}{5}$,$1+(2× 3-4÷ 5)=\dfrac{31}{5}$,$1+2× (3-4)÷ 5=\dfrac{3}{5}$,$1+2× (3-4÷ 5)=\dfrac{27}{5}$,$1+2× 3-(4÷5)=\dfrac{31}{5}$,$(1+2)× (3-4)÷ 5=-\dfrac{3}{5}$,$(1+2)× (3-4÷ 5)=\dfrac{33}{5}$,$(1+2)× 3-(4÷ 5)=\dfrac{41}{5}$.
观察以上结果发现:至少存在一种“加括号操作”的运算结果是$\dfrac{7}{5}$,故①正确;不存在任何“加括号操作”的运算结果是$\dfrac{26}{5}$,故②正确;所有“加括号操作”共有7种不同的运算结果,即$\dfrac{41}{5}$,$\dfrac{31}{5}$,$\dfrac{3}{5}$,$\dfrac{7}{5}$,$\dfrac{27}{5}$,$-\dfrac{3}{5}$,$\dfrac{33}{5}$,故③正确.故选D.
查看更多完整答案,请扫码查看


