《2025年新课程学习指导七年级数学上册华东师大版》

四、画出数轴，并在数轴上表示下列各数及它们的相反数
$-4\frac{1}{4}, 2, 0, -3, 1$

答案：
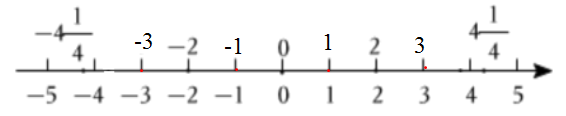
解：如图所示

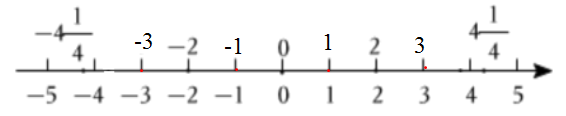
五、操作与尝试:在纸面上有如图所示的数轴，折叠纸面，若数轴上数5表示的点与数-5表示的点重合，则数轴上数-1表示的点与数1表示的点重合.

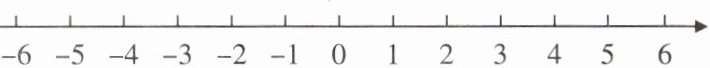
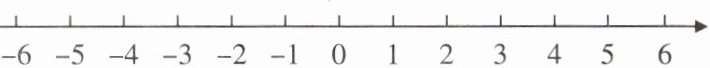
探究与应用:现打开纸面后，再次折叠，使数轴上数2表示的点与数0表示的点重合. 数轴上$A、B$两点折叠后重合，$M、N$两点折叠后重合.
1. 则数轴上数-4表示的点与数6表示的点重合;
2. 若点$A$到原点的距离是3个单位长度，求$B$点表示的数;
3. 若数轴上$M、N$两点之间的距离为2024,且$M$点表示的数比$N$点表示的数小，求$M$点、$N$点表示的数.

答案： 探究与应用：
折叠后2与0重合，对称轴为两点中点：$\frac{2+0}{2}=1$，即对称轴为1。
1.
设与-4重合的点为$x$，则$\frac{-4+x}{2}=1$，解得$x=6$。
答案：6
2.
点A到原点距离为3，故A表示的数为3或-3。
若A=3，设B=x，则$\frac{3+x}{2}=1$，解得$x=-1$；
若A=-3，设B=x，则$\frac{-3+x}{2}=1$，解得$x=5$。
B点表示的数为-1或5
3.
设M=a，N=b（$a＜b$），M、N关于1对称且距离2024，
则$\begin{cases}\frac{a+b}{2}=1\\b-a=2024\end{cases}$，
解得$a=-1011$，$b=1013$。
M=-1011，N=1013
答案：
1. 6
2. -1或5
3. M=-1011，N=1013

【例】求下列各数的绝对值：$\frac{2}{3}, -6\frac{1}{2}, \pi - 3.2$.
点拨：求一个数$a$的绝对值，首先要判断$a$是正数、负数，还是$0$. 此题中，$\frac{2}{3}$是正数，$-6\frac{1}{2}$是负数，$\pi - 3.2$也是负数.
 

答案： 解：$\left|\frac{2}{3}\right|=\frac{2}{3}$
$\left|-6\frac{1}{2}\right|=6\frac{1}{2}$
$|\pi - 3.2|=3.2 - \pi$

1. $-4$的绝对值是4.

答案： 4（题目中要求填在特定位置，若按常规答案形式，此处明确答案为4 ）

2. $-52$的绝对值是52，相反数是52；绝对值等于$7$的数是±7.

答案： 52；52；±7

3. 求绝对值：$\left|-\frac{1}{2}\right| =$$\frac{1}{2}$（或 0.5），$|+5| =$5，$|0| =$0.

答案： $\frac{1}{2}$（或 0.5）；5；0。

4. 在$-5, -\frac{17}{3}, -\frac{23}{4}$中，绝对值最小的数是是$-5$.

答案： $-5$