第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
4. 七巧板是我国一种传统智力玩具,是中国劳动人民智慧的结晶. 它由如图3所示的七块板组成,可以拼成许多图形,右图是用左图中的3块拼成的小船.若左图中正方形$ABCD$的面积为4,则右图中小船的面积为
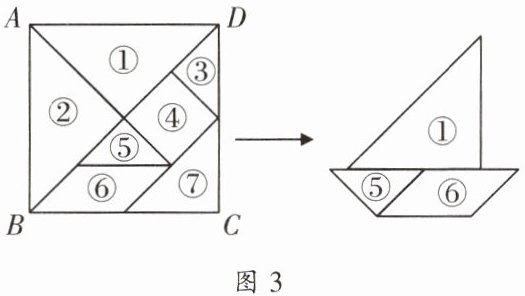
2
.
答案:
2
1. 在长方形、长方体、三角形、球、六边形、圆中,有(
A.3
B.4
C.5
D.6
B
)个平面图形.A.3
B.4
C.5
D.6
答案:
B
2. 从正方体中切下一块,得到的切口图形中,边数最多的多边形是 (
A.四边形
B.五边形
C.六边形
D.七边形
C
)A.四边形
B.五边形
C.六边形
D.七边形
答案:
C
3. 图4中有(
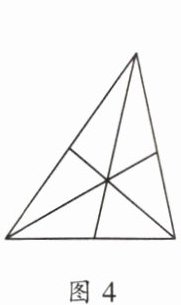
A.15
B.16
C.17
D.18
B
)个三角形.
A.15
B.16
C.17
D.18
答案:
B
三、画出五边形$ABCDE$, 试用不同的方法把这个五边形分割成三角形,至少可以分割成多少个三角形? 请试一试.
答案:
至少可以分割成$3$个三角形。
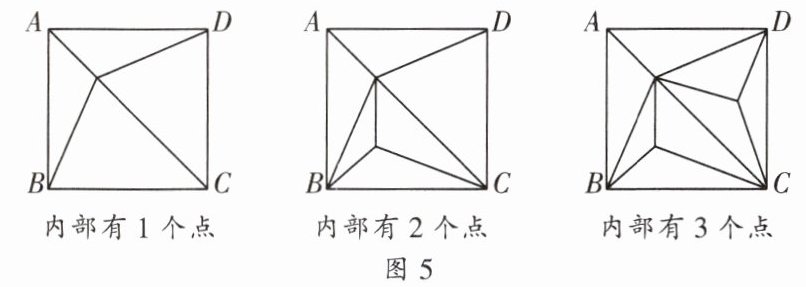
四、如图5,正方形$ABCD$内部有若干个点,用这些点以及正方形$ABCD$的顶点$A$、$B$、$C$、$D$把原正方形分割成一些三角形(互不重叠).
1. 填写下表.
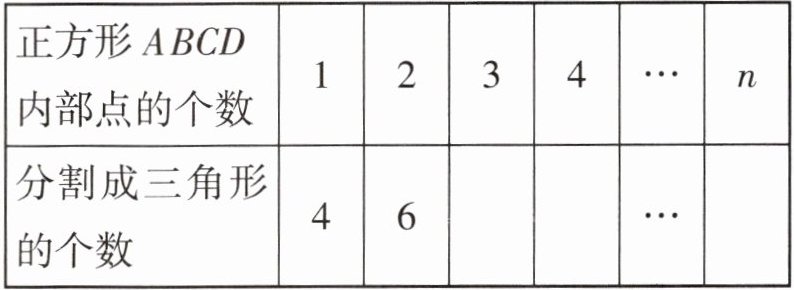
| 正方形$ABCD$内部点的个数 | 1 | 2 | 3 | 4 | $n$ |
| -- | -- | -- | -- | -- | -- |
| 分割成三角形的个数 |
2. 原正方形能否被分割成2024个三角形?若能,求此时正方形$ABCD$内部有多少个点;若不能,请说明理由.
1. 填写下表.

| 正方形$ABCD$内部点的个数 | 1 | 2 | 3 | 4 | $n$ |
| -- | -- | -- | -- | -- | -- |
| 分割成三角形的个数 |
4
| 6
| 8
| 10
| $2n + 2$
|2. 原正方形能否被分割成2024个三角形?若能,求此时正方形$ABCD$内部有多少个点;若不能,请说明理由.

假设能被分割成2024个三角形,令$2n + 2 = 2024$,解得$2n=2022$,$n = 1011$。所以原正方形能被分割成2024个三角形,此时正方形$ABCD$内部有1011个点。
答案:
1.
| 正方形$ABCD$内部点的个数 | 1 | 2 | 3 | 4 | $·s$ | $n$ |
| -- | -- | -- | -- | -- | -- | -- |
| 分割成三角形的个数 | 4 | 6 | 8 | 10 | $·s$ | $2n + 2$ |
2. 假设能被分割成$2024$个三角形,令$2n + 2 = 2024$,
解得$2n=2022$,$n = 1011$。
所以原正方形能被分割成$2024$个三角形,此时正方形$ABCD$内部有$1011$个点。
| 正方形$ABCD$内部点的个数 | 1 | 2 | 3 | 4 | $·s$ | $n$ |
| -- | -- | -- | -- | -- | -- | -- |
| 分割成三角形的个数 | 4 | 6 | 8 | 10 | $·s$ | $2n + 2$ |
2. 假设能被分割成$2024$个三角形,令$2n + 2 = 2024$,
解得$2n=2022$,$n = 1011$。
所以原正方形能被分割成$2024$个三角形,此时正方形$ABCD$内部有$1011$个点。
查看更多完整答案,请扫码查看


