第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
三、如图 9,已知$\angle AOC = \angle BOD = 78^{\circ}$,$\angle BOC =$
$35^{\circ}$,求$\angle AOD$ 的度数.
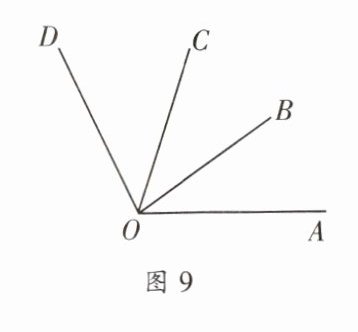
$35^{\circ}$,求$\angle AOD$ 的度数.

答案:
$\because \angle AOC = \angle BOD = 78°$,$\angle BOC = 35°$,
$\therefore \angle AOB = \angle AOC - \angle BOC = 78° - 35° = 43°$,
$\therefore \angle AOD = \angle BOD + \angle AOB = 78° + 43° = 121°$。
$\angle AOD=121°$。
$\therefore \angle AOB = \angle AOC - \angle BOC = 78° - 35° = 43°$,
$\therefore \angle AOD = \angle BOD + \angle AOB = 78° + 43° = 121°$。
$\angle AOD=121°$。
四、如图 10,已知 $\angle A$,$\angle B$,用尺规作图作一
个$\angle C$,使$\angle C = \angle A - \angle B$.(不写作法,保
留作图痕迹)
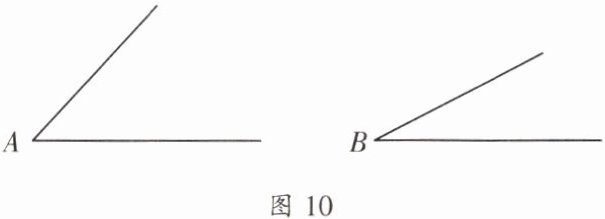
个$\angle C$,使$\angle C = \angle A - \angle B$.(不写作法,保
留作图痕迹)

答案:
解:如图所示,∠DCE即为所求
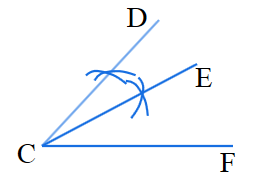
解:如图所示,∠DCE即为所求

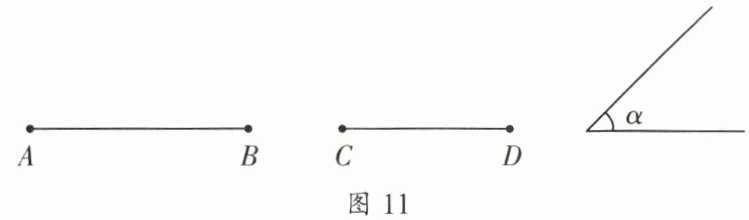
五、如图 11 所示,已知线段 $AB$,线段 $CD$,$\angle \alpha$,
作$\angle EAB = \angle \alpha$,$\angle \alpha$ 的两边分别等于线段
$AB$,线段 $CD$,试用尺规作图作出满足条
件的三角形.(不写作法,保留作图痕迹)
作$\angle EAB = \angle \alpha$,$\angle \alpha$ 的两边分别等于线段
$AB$,线段 $CD$,试用尺规作图作出满足条
件的三角形.(不写作法,保留作图痕迹)

答案:
解:如图所示
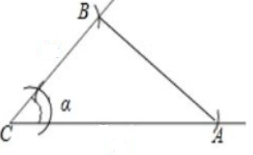
解:如图所示

1. 若$\angle \alpha=53^{\circ}20'$,则$\angle \alpha$的余角是
$36^{\circ}40'$
,$\angle \alpha$的补角是$126^{\circ}40'$
.
答案:
余角是 $36^{\circ}40'$,补角是 $126^{\circ}40'$(答案处分别填写余角和补角的结果,根据格式要求只填具体值)。
余角是 $36^{\circ}40'$,补角是 $126^{\circ}40'$(答案处分别填写余角和补角的结果,根据格式要求只填具体值)。
2. 一个角的补角是这个角的3倍,这个角的度数为
45°
.
答案:
$45^{\circ}$(填数字,按照题目要求此处应只填数值相关,若题目是填空形式)若为选择题形式对应选项按实际来,本题按解析直接给度数答案。
3. 若$\angle A+\angle B=180^{\circ}$,$\angle D+\angle C=180^{\circ}$,且$\angle A=\angle C$,则
$\angle B=\angle D$
.
答案:
$\angle B=\angle D$
4. 一个角等于它的余角,则这个角是
45°
.
答案:
45°
1. 如图12,点$O$在直线$AB$上,若$\angle 1=40^{\circ}$,则$\angle 2$的度数是
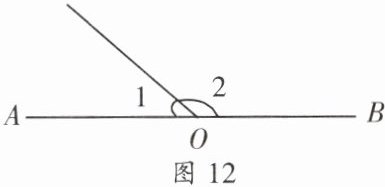
A.$50^{\circ}$
B.$60^{\circ}$
C.$140^{\circ}$
D.$150^{\circ}$
C

A.$50^{\circ}$
B.$60^{\circ}$
C.$140^{\circ}$
D.$150^{\circ}$
答案:
C
2. 如图13,已知$\angle ACB=90^{\circ}$,$\angle 1=\angle B$,$\angle 2=\angle A$,则下列说法错误的是
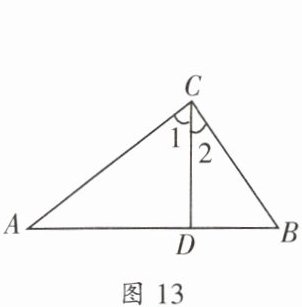
A.$\angle A$与$\angle B$不互为余角
B.$\angle 1$与$\angle 2$互为余角
C.$\angle 2$与$\angle B$互为余角
D.$\angle 1$与$\angle A$互为余角
A

A.$\angle A$与$\angle B$不互为余角
B.$\angle 1$与$\angle 2$互为余角
C.$\angle 2$与$\angle B$互为余角
D.$\angle 1$与$\angle A$互为余角
答案:
A
3. 一副三角板按如图14所示方式摆放,且$\angle 1$比$\angle 2$大$40^{\circ}$,则$\angle 2$的度数是 (
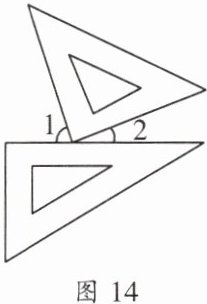
A.$20^{\circ}$
B.$25^{\circ}$
C.$40^{\circ}$
D.$50^{\circ}$
B
)
A.$20^{\circ}$
B.$25^{\circ}$
C.$40^{\circ}$
D.$50^{\circ}$
答案:
B
4. 如果$\angle \alpha+\angle \beta=90^{\circ}$,$\angle \beta+\angle \gamma=90^{\circ}$,那么$\angle \alpha$与$\angle \gamma$的关系是 (
A.$\angle \alpha+\angle \gamma=90^{\circ}$
B.$\angle \alpha+\angle \gamma=180^{\circ}$
C.$\angle \alpha=\angle \gamma$
D.不能确定
C
)A.$\angle \alpha+\angle \gamma=90^{\circ}$
B.$\angle \alpha+\angle \gamma=180^{\circ}$
C.$\angle \alpha=\angle \gamma$
D.不能确定
答案:
C
查看更多完整答案,请扫码查看


