《2025年新课程学习指导七年级数学上册华东师大版》

2. 如图 11，$OB \perp OD$，$OC \perp OA$，$\angle BOC=32°$，则 $\angle AOD$ 的度数为 (A)

A.$148°$
B.$132°$
C.$128°$
D.$90°$

答案： A

3. 将一块长方形纸片，按如图 12 所示的方式折叠，$BC$、$BD$ 为折痕，则 $\angle CBD$ 的度数为 (C)

A.$60°$
B.$75°$
C.$90°$
D.$95°$

答案： C

三、如图 13，利用三角板过点 $P$ 分别向 $\angle AOB$ 的两边或两边的延长线作垂线.

答案：
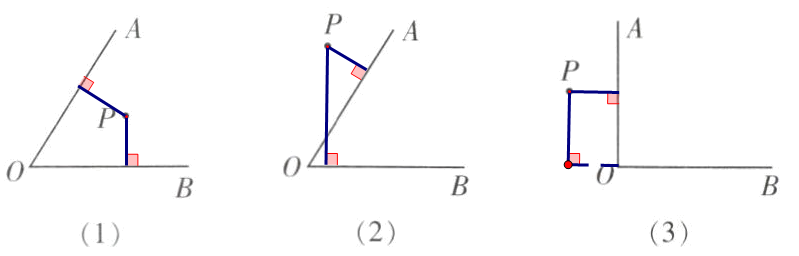
解：如图所示

四、如图 14，已知 $AO \perp CO$，$\angle COD=40°$，$\angle BOC=\angle AOD$.试说明 $OB \perp OD$.
请完善解答过程，并在括号内填上相应依据：
解：因为 $AO \perp CO$，
所以 $\angle AOC=$90°（垂直的定义）.
又因为 $\angle COD=40°$（已知），
所以 $\angle AOD=$$\angle AOC - \angle COD = 90^{\circ} - 40^{\circ} = 50^{\circ}$.
又因为 $\angle BOC=\angle AOD$（已知），
所以 $\angle BOD=$$\angle BOC + \angle COD = 50^{\circ} + 40^{\circ} = 90^{\circ}$，
所以OB$\perp$OD（垂直的定义）.

答案： 因为 $AO \perp CO$，
所以 $\angle AOC=90^{\circ}$（垂直的定义）.
又因为 $\angle COD=40^{\circ}$（已知），
所以 $\angle AOD=\angle AOC - \angle COD = 90^{\circ} - 40^{\circ} = 50^{\circ}$.
又因为 $\angle BOC=\angle AOD$（已知），
所以 $\angle BOC = 50^{\circ}$，
所以 $\angle BOD = \angle BOC + \angle COD = 50^{\circ} + 40^{\circ} = 90^{\circ}$，
所以 $OB \perp OD$（垂直的定义）.

五、如图 15，三条直线 $AB$、$CD$、$EF$ 相交于点 $O$，$\angle1=50°$，$\angle2=40°$，试判断直线 $AB$ 与 $EF$ 的位置关系，并说明理由.

答案： $AB \bot EF$，理由：
因为$\angle 1 = 50°$，$\angle 2 = 40°$，
则$\angle 1+\angle 2 = 90°$。
则$\angle 3=180° - (\angle 1+\angle 2) = 90°$，
即$AB \bot EF$。

1. 如图16，直线$DE$截直线$AB$和$BC$，$\angle1$与$\angle2$是同位角，$\angle3$与$\angle4$是内错角，$\angle2$与$\angle3$是同旁内角.
 

答案： 【解析】：直线DE截直线AB和BC，截线为DE，被截线为AB、BC。
∠1与∠2：∠1在截线DE上方、被截线BC左侧，∠2在截线DE下方、被截线AB左侧，位置在截线同侧、被截线两侧，是同位角。
∠3与∠4：∠3在截线DE上方、被截线AB右侧，∠4在截线DE下方、被截线AB右侧，位置在截线两侧、被截线之间，是内错角。
∠2与∠3：∠2在截线DE下方、被截线AB左侧，∠3在截线DE上方、被截线AB右侧，位置在截线两侧、被截线之间，是同旁内角。
【答案】：同位角；内错角；同旁内角

2. 如图17，根据图形填空：
(1)若$ED$，$BF$被$AB$所截，则$\angle1$与∠2是同位角；
(2)若$ED$，$BC$被$AF$所截，则$\angle3$与∠4是内错角；
(3)$\angle1$与$\angle3$是$AB$和$AF$被ED所截构成的同位角；
(4)$\angle2$与$\angle4$是AB和AF被$BC$所截构成的同旁内角.

答案： ∠2；∠4；ED，同位；AB，AF，同旁内