《2025年新课程学习指导七年级数学上册华东师大版》

5. 一台电视机原价是 2 500 元，现按原价的 8 折出售，则购买$a$台这样的电视机需要2000a元.

答案：
$2000a$

1. 长方形的周长为$c$米，宽为$x$米，则长为
(D)

A.$(c - 2x)$米
B.$(\frac{c}{2} - 2x)$米
C.$\frac{c - x}{2}$米
D.$\frac{c - 2x}{2}$米

答案： D

2. 购买 1 个单价为$a$元的面包和 3 瓶单价为$b$元的饮料，所需钱数为
(D)

A.$(a + b)$元
B.$[3(a + b)]$元
C.$(3a + b)$元
D.$(a + 3b)$元

答案： D

3. 一个两位数，十位上的数字是$x$，个位上的数字是$y$，则这个两位数是
(C)

A.$xy$
B.$10(x + y)$
C.$10x + y$
D.$10y + x$

答案： C

4. 受季节影响，某种商品每件按售价降价 10% 后，又降价$a$元，现在每件售价为$b$元，那么该商品每件的原售价为(A)元.

A.$\frac{a + b}{1 - 10\%}$
B.$(1 - 10\%)(a + b)$
C.$\frac{b - a}{1 - 10\%}$
D.$(1 - 10\%)(a - b)$

答案： A

三、解答题
小明坐计程车，发现：

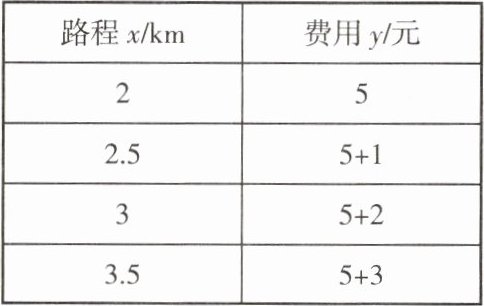
请用$x$表示$y$.

答案： 当$x \geq 2$时，
由表格数据可知：起步路程2km对应费用5元，每增加0.5km费用增加1元，即每公里费用为2元。
超出2km的路程为$(x - 2)$km，超出费用为$2(x - 2)$元，
总费用$y = 5 + 2(x - 2)$，化简得$y = 2x + 1$。
验证：当$x = 2$时，$y = 2×2 + 1 = 5$；当$x = 2.5$时，$y = 2×2.5 + 1 = 6$；当$x = 3$时，$y = 2×3 + 1 = 7$；当$x = 3.5$时，$y = 2×3.5 + 1 = 8$，均符合表格数据。
结论：$y = 2x + 1$。

四、如图，一块长为$a$m，宽为$b$m的长方形草坪中间有一条宽为 1 m 的人行道. 求这块草坪实际的绿化面积.（单位：m）

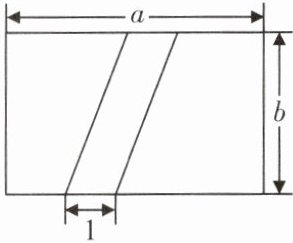
答案： 绿化面积 = 长方形草坪面积 - 人行道面积
长方形草坪面积 = $a × b = ab$（m²）
人行道面积 = $1 × b = b$（m²）
绿化面积 = $ab - b$（m²）
答：这块草坪实际的绿化面积为$(ab - b)$m²。

1. 用语言叙述代数式$\frac {2x+y}{3}$的意义为$x$的2倍与$y$的和除以3（答案不唯一）。
_.

答案： $x$的2倍与$y$的和除以3（答案不唯一）。

2. 用代数式表示：比$7a$大1的数是$7a + 1$；被5除商$m+2$余1的数是$5m + 11$.

答案： $7a + 1$；$5m + 11$

3. 设甲数为$x$，乙数为$y$，用代数式表示：(1)甲、乙两数的和除以甲、乙两数的积：$\frac{x + y}{xy}$； (2)比甲数除以乙数的商的一半小3的数：$\frac{x}{2y}-3$.

答案：
(1) $\frac{x + y}{xy}$；
(2) $\frac{x}{2y}-3$。

4. 从甲地到乙地航行的路程为$S$千米，一艘轮船的静水速度为$a$千米/小时，水流速度为$b$千米/小时，则轮船从甲地到乙地逆流而上需要$\frac{S}{a-b}$小时；轮船从乙地到甲地顺流而下需要$\frac{S}{a+b}$小时.

答案：
逆流而上需要 $\boxed{\frac{S}{a-b}}$
顺流而下需要 $\boxed{\frac{S}{a+b}}$

1. 有下列式子：$2ab-1$，$\pi r^2$，$x+1=0$，100，$a-b＜0$，$S=ab$，$(a+b)(a-b)$，$\frac {x^2+y^3}2$，$\frac{S}{v}$.其中代数式的个数是
(A)

A.6
B.7
C.8
D.9

答案： A

2. 下列说法正确的是　　　　　　(B)

A.代数式$(x-y)^2$与$x^2-y^2$的意义相同
B.代数式$\frac{1}{2}x$与$\frac{x}{2}$的意义相同
C.代数式$3(a+2)$的意义是：$a$的3倍与2的和
D.代数式$\frac{m+n}{m-n}$的意义是：$m$、$n$的和除$m$、$n$的差

答案： B