《2025年新课程学习指导七年级数学上册华东师大版》

三、把下列各数用“$＞$”号连接起来
$-\frac{2}{5}$，$0$，$-(-\frac{7}{8})$，$+(-\frac{6}{7})$，$-|-12|$，$+(+0.2)$，$-(+0.01)$

答案： 首先化简各数：
$-\left(-\frac{7}{8}\right) = \frac{7}{8}$，
$+\left(-\frac{6}{7}\right) = -\frac{6}{7}$，
$-|-12| = -12$，
$+(+0.2) = 0.2$，
$-(+0.01) = -0.01$，
$-\frac{2}{5} = -0.4$，
$0 = 0$。
接下来，根据有理数大小比较的规则（正数大于0，0大于负数，正数之间比较绝对值越大值越大，负数之间比较绝对值越大小数反而大（绝对值大的负数更小））进行排序：
$\frac{7}{8} ＞ 0.2 ＞ 0 ＞ -0.01 ＞ -0.4 ＞ -\frac{6}{7} ＞ -12$，
即：
$- \left( - \frac{7}{8} \right) ＞ + \left( + 0.2 \right) ＞ 0 ＞ - \left( + 0.01 \right) ＞ - \frac{2}{5} ＞ + \left( - \frac{6}{7} \right) ＞ - |-12|$。

四、从下图中最小的数开始，由小到大依次用线连接起来，看看你画的是什么

答案：
解：如图

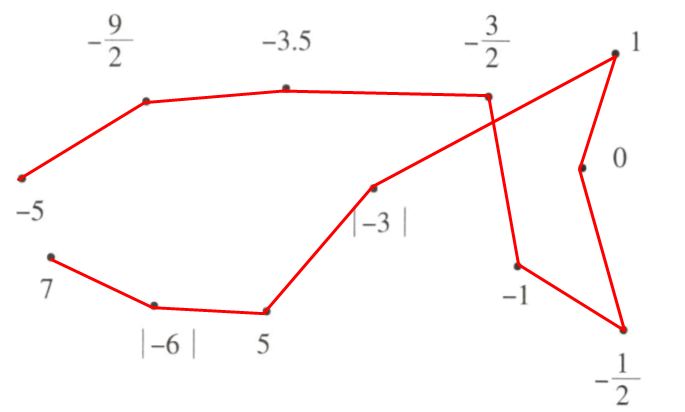
连线后形成的图案是小鱼。

五、小马在写作业时不慎将墨水滴在数轴上，如图所示，根据图中的信息可知，被墨水遮住的最大负整数是-1，最小负整数是-6，最大正整数是3.

答案： -1,-6,3

六、$|x-2|+10$的最小值是10，此时$x=$2.

答案： 10；2

【例 1】计算：$\left( + \frac { 3 } { 4 } \right) + 4 . 1 + \frac { 1 } { 2 } + \left( - \frac { 1 } { 4 } \right) + ( - 1 0 . 1 ) + \left( - \frac { 3 } { 4 } \right) + 7$
点拨：多个数相加时，先观察各数间能否凑整、凑零，再利用加法交换律和结合律，改变加法顺序和组合进行计算.
 

答案： 解：原式$=\left[\left(+\frac{3}{4}\right)+\left(-\frac{3}{4}\right)\right]+\left[4.1+\left(-10.1\right)\right]+\left[\frac{1}{2}+\left(-\frac{1}{4}\right)\right]+7$
$=0+\left(-6\right)+\frac{1}{4}+7$
$=\left(-6+7\right)+\frac{1}{4}$
$=1+\frac{1}{4}$
$=1\frac{1}{4}$