第91页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
1. (北京中考)正十二边形的外角和为(
A.$30^{\circ}$
B.$150^{\circ}$
C.$360^{\circ}$
D.$1800^{\circ}$
C
)A.$30^{\circ}$
B.$150^{\circ}$
C.$360^{\circ}$
D.$1800^{\circ}$
答案:
C
2. (枣庄中考)如图,一束太阳光线平行照射在放置于地面的正六边形上,若 $\angle1 = 44^{\circ}$,则 $\angle2$ 的度数为(
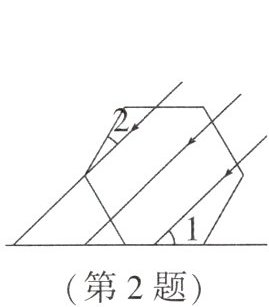
A.$14^{\circ}$
B.$16^{\circ}$
C.$24^{\circ}$
D.$26^{\circ}$
B
)
A.$14^{\circ}$
B.$16^{\circ}$
C.$24^{\circ}$
D.$26^{\circ}$
答案:
B
3. (雅安中考)如图,六边形 $ABCDEF$ 为正六边形,四边形 $ABGH$ 为正方形,连接 $CG$,则 $\angle BCG+\angle BGC = $
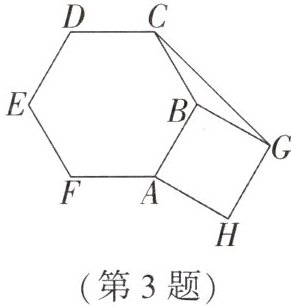
$30^{\circ}$
.
答案:
$30^{\circ}$
4. (烟台中考)一个多边形截去一个角后,形成另一个多边形的内角和为 $720^{\circ}$,那么原多边形的边数为
5或6或7
.
答案:
5或6或7
5. 如图所示的图形是一个轴对称图形,经过点 $A_1$,$A_5$ 的直线是它的对称轴,已知 $\angle A_2= \angle A_8 = 90^{\circ}$,$\angle A_3= \angle A_4= \angle A_5= \angle A_6= \angle A_7 = 135^{\circ}$,如果把大于平角的角称为“优角”,求优角 $\angle A_1$ 的度数.
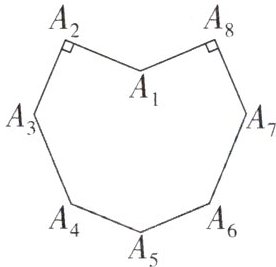

答案:
$225^{\circ}$ 解析:如图所示,作对称轴$A_{1}A_{5}$,
∵经过点$A_{1}$,$A_{5}$的直线是它的对称轴,已知$\angle A_{2}=\angle A_{8}=90^{\circ}$,$\angle A_{3}=\angle A_{4}=\angle A_{5}=\angle A_{6}=\angle A_{7}=135^{\circ}$,
∴$\angle A_{1}A_{5}A_{4}=\frac{1}{2}×135^{\circ}=67.5^{\circ}$,"优角$\angle A_{2}A_{1}A_{8}$"=$2×[(5 - 2)×180^{\circ}-90^{\circ}-2×135^{\circ}-67.5^{\circ}]=225^{\circ}$.
∵经过点$A_{1}$,$A_{5}$的直线是它的对称轴,已知$\angle A_{2}=\angle A_{8}=90^{\circ}$,$\angle A_{3}=\angle A_{4}=\angle A_{5}=\angle A_{6}=\angle A_{7}=135^{\circ}$,
∴$\angle A_{1}A_{5}A_{4}=\frac{1}{2}×135^{\circ}=67.5^{\circ}$,"优角$\angle A_{2}A_{1}A_{8}$"=$2×[(5 - 2)×180^{\circ}-90^{\circ}-2×135^{\circ}-67.5^{\circ}]=225^{\circ}$.
6. (河北中考改编)(1)如图①,平面上,将边长相等的正三角形、正方形的一边重合并叠在一起,则 $\angle1= $
(2)如图②,平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,则 $\angle1-\angle2+\angle3= $
(3)如图③,平面上,将边长相等的正三角形、正方形、正五边形、正六边形……正 $(n + 3)$ 边形的一边重合并叠在一起,每个正 $(k + 3)$ 边形与正 $(k + 2)$ 边形的重合边的同一侧的邻边的夹角为 $\angle k$,试说明 $\angle1-\angle2+\angle3-\angle4+…+\angle(n - 1)-\angle n$ 的大小不会小于 $12^{\circ}$($n$ 是偶数).
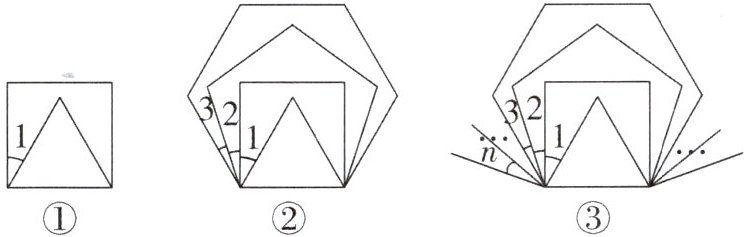
$30^{\circ}$
.(2)如图②,平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,则 $\angle1-\angle2+\angle3= $
$24^{\circ}$
.(3)如图③,平面上,将边长相等的正三角形、正方形、正五边形、正六边形……正 $(n + 3)$ 边形的一边重合并叠在一起,每个正 $(k + 3)$ 边形与正 $(k + 2)$ 边形的重合边的同一侧的邻边的夹角为 $\angle k$,试说明 $\angle1-\angle2+\angle3-\angle4+…+\angle(n - 1)-\angle n$ 的大小不会小于 $12^{\circ}$($n$ 是偶数).

正$n$边形的每个内角为$\frac{(n - 2)×180^{\circ}}{n}=180^{\circ}-\frac{360^{\circ}}{n}$,从而对于不超过$n$的自然数$k$,$\angle k=(180^{\circ}-\frac{360^{\circ}}{k + 3})-(180^{\circ}-\frac{360^{\circ}}{k + 2})=360^{\circ}×(\frac{1}{k + 2}-\frac{1}{k + 3})$,从而$\angle1-\angle2+\angle3-\angle4+\cdots+\angle(n - 1)-\angle n=360^{\circ}×[(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{6})-\cdots-(\frac{1}{n + 2}-\frac{1}{n + 3})]$ 首先注意到$360^{\circ}×[(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})]=12^{\circ}$.而$(\frac{1}{n}-\frac{1}{n + 1})-(\frac{1}{n + 1}-\frac{1}{n + 2})=2(n + 1)[\frac{1}{n(n + 2)}-\frac{1}{(n + 1)^{2}}]=\frac{2}{n(n + 1)(n + 2)}>0$,从而$360^{\circ}×[(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{6})-\cdots-(\frac{1}{n + 2}-\frac{1}{n + 3})]>360^{\circ}×[(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})]=12^{\circ}$.所以$\angle1-\angle2+\angle3-\angle4+\cdots+\angle(n - 1)-\angle n$的大小不会小于$12^{\circ}$.
答案:
(1)$30^{\circ}$
(2)$24^{\circ}$
(3)正$n$边形的每个内角为$\frac{(n - 2)×180^{\circ}}{n}=180^{\circ}-\frac{360^{\circ}}{n}$,从而对于不超过$n$的自然数$k$,$\angle k=(180^{\circ}-\frac{360^{\circ}}{k + 3})-(180^{\circ}-\frac{360^{\circ}}{k + 2})=360^{\circ}×(\frac{1}{k + 2}-\frac{1}{k + 3})$,从而$\angle1-\angle2+\angle3-\angle4+\cdots+\angle(n - 1)-\angle n=360^{\circ}×[(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{6})-\cdots-(\frac{1}{n + 2}-\frac{1}{n + 3})]$ 首先注意到$360^{\circ}×[(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})]=12^{\circ}$.而$(\frac{1}{n}-\frac{1}{n + 1})-(\frac{1}{n + 1}-\frac{1}{n + 2})=2(n + 1)[\frac{1}{n(n + 2)}-\frac{1}{(n + 1)^{2}}]=\frac{2}{n(n + 1)(n + 2)}>0$,从而$360^{\circ}×[(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{6})-\cdots-(\frac{1}{n + 2}-\frac{1}{n + 3})]>360^{\circ}×[(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})]=12^{\circ}$.所以$\angle1-\angle2+\angle3-\angle4+\cdots+\angle(n - 1)-\angle n$的大小不会小于$12^{\circ}$.
(1)$30^{\circ}$
(2)$24^{\circ}$
(3)正$n$边形的每个内角为$\frac{(n - 2)×180^{\circ}}{n}=180^{\circ}-\frac{360^{\circ}}{n}$,从而对于不超过$n$的自然数$k$,$\angle k=(180^{\circ}-\frac{360^{\circ}}{k + 3})-(180^{\circ}-\frac{360^{\circ}}{k + 2})=360^{\circ}×(\frac{1}{k + 2}-\frac{1}{k + 3})$,从而$\angle1-\angle2+\angle3-\angle4+\cdots+\angle(n - 1)-\angle n=360^{\circ}×[(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{6})-\cdots-(\frac{1}{n + 2}-\frac{1}{n + 3})]$ 首先注意到$360^{\circ}×[(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})]=12^{\circ}$.而$(\frac{1}{n}-\frac{1}{n + 1})-(\frac{1}{n + 1}-\frac{1}{n + 2})=2(n + 1)[\frac{1}{n(n + 2)}-\frac{1}{(n + 1)^{2}}]=\frac{2}{n(n + 1)(n + 2)}>0$,从而$360^{\circ}×[(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{6})-\cdots-(\frac{1}{n + 2}-\frac{1}{n + 3})]>360^{\circ}×[(\frac{1}{3}-\frac{1}{4})-(\frac{1}{4}-\frac{1}{5})]=12^{\circ}$.所以$\angle1-\angle2+\angle3-\angle4+\cdots+\angle(n - 1)-\angle n$的大小不会小于$12^{\circ}$.
查看更多完整答案,请扫码查看


