第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
9. 如图,在梯形$ABCD$中,$AB// CD$,$\angle BAD = 90^{\circ}$,$AB = 6$,对角线$AC平分\angle BAD$,点$E在AB$上,且$AE = 2$($AE < AD$),$P是AC$上的动点,则$PE + PB$的最小值是
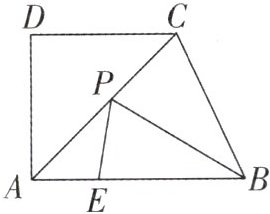
$2\sqrt{10}$
。
答案:
$2\sqrt{10}$
10. 已知点$A(1,3)$,$B(5,-2)$,在$x轴上找一点P$,使 (1) $AP + BP$最小;(2) $|AP - BP|$最小;(3) $|AP - BP|$最大。
答案:
(1)如图①,连接AB,则直线AB交x轴于点P,设$P(x,0)$,过A,B两点的直线为$y=kx+b(k\neq0)$,则$\begin{cases}3 = k + b\\-2 = 5k + b\end{cases}$,解得$\begin{cases}k = -\frac{5}{4}\\b = \frac{17}{4}\end{cases}$,故过A,B两点的一次函数的表达式为$y=-\frac{5}{4}x+\frac{17}{4}$,把点$P(x,0)$代入一次函数的表达式得$-\frac{5}{4}x+\frac{17}{4}=0$,解得$x=\frac{17}{5}$,故点P的坐标为$(\frac{17}{5},0)$。

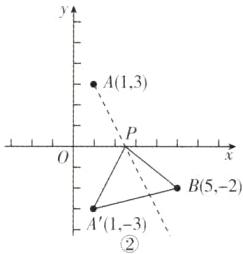
(2)因为$|AP - BP|\geq0$,所以当$AP = BP$时,$|AP - BP|$最小,故点P在线段AB的垂直平分线上。如图②,作线段AB的垂直平分线交x轴于点P,则点P即为所求,作点A关于x轴的对称点$A'$,连接$A'P$。设$P(x,0)$,则$PA' = PB$,即$\sqrt{(1 - x)^{2}+(-3)^{2}}=\sqrt{(5 - x)^{2}+(-2)^{2}}$,解得$x=\frac{19}{8}$,故点P的坐标为$(\frac{19}{8},0)$。
(3)如图③,作点A关于x轴的对称点$A'$(也可以作B关于x轴的对称点$B'$,道理一样),这样AP始终等于$A'P$,若点$A'$,P,B构成三角形,则$0<|AP - BP|<A'B$,其实右边可以取等号,也就是当P点为直线$A'B$与x轴的交点时取等号,这时$|AP - BP|$最大,等于$A'B$。设$P(x,0)$,过$A'$,B两点的直线为$y=kx+b(k\neq0)$,故$\begin{cases}-2 = 5k + b\\-3 = k + b\end{cases}$,解得$\begin{cases}k = \frac{1}{4}\\b = -\frac{13}{4}\end{cases}$,故过$A'$,B两点的直线表达式为$y=\frac{1}{4}x-\frac{13}{4}$,把$P(x,0)$代入得,$\frac{1}{4}x-\frac{13}{4}=0$,解得$x = 13$,故点P坐标为$(13,0)$。

(1)如图①,连接AB,则直线AB交x轴于点P,设$P(x,0)$,过A,B两点的直线为$y=kx+b(k\neq0)$,则$\begin{cases}3 = k + b\\-2 = 5k + b\end{cases}$,解得$\begin{cases}k = -\frac{5}{4}\\b = \frac{17}{4}\end{cases}$,故过A,B两点的一次函数的表达式为$y=-\frac{5}{4}x+\frac{17}{4}$,把点$P(x,0)$代入一次函数的表达式得$-\frac{5}{4}x+\frac{17}{4}=0$,解得$x=\frac{17}{5}$,故点P的坐标为$(\frac{17}{5},0)$。


(2)因为$|AP - BP|\geq0$,所以当$AP = BP$时,$|AP - BP|$最小,故点P在线段AB的垂直平分线上。如图②,作线段AB的垂直平分线交x轴于点P,则点P即为所求,作点A关于x轴的对称点$A'$,连接$A'P$。设$P(x,0)$,则$PA' = PB$,即$\sqrt{(1 - x)^{2}+(-3)^{2}}=\sqrt{(5 - x)^{2}+(-2)^{2}}$,解得$x=\frac{19}{8}$,故点P的坐标为$(\frac{19}{8},0)$。
(3)如图③,作点A关于x轴的对称点$A'$(也可以作B关于x轴的对称点$B'$,道理一样),这样AP始终等于$A'P$,若点$A'$,P,B构成三角形,则$0<|AP - BP|<A'B$,其实右边可以取等号,也就是当P点为直线$A'B$与x轴的交点时取等号,这时$|AP - BP|$最大,等于$A'B$。设$P(x,0)$,过$A'$,B两点的直线为$y=kx+b(k\neq0)$,故$\begin{cases}-2 = 5k + b\\-3 = k + b\end{cases}$,解得$\begin{cases}k = \frac{1}{4}\\b = -\frac{13}{4}\end{cases}$,故过$A'$,B两点的直线表达式为$y=\frac{1}{4}x-\frac{13}{4}$,把$P(x,0)$代入得,$\frac{1}{4}x-\frac{13}{4}=0$,解得$x = 13$,故点P坐标为$(13,0)$。

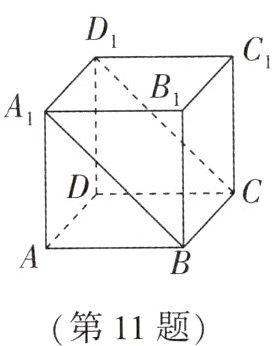
11. (孝感自主招生)如图,在棱长为 1 的正方体$ABCD - A_1B_1C_1D_1$中,一只蚂蚁从点$A$出发,沿正方体表面爬行到面对角线$A_1B上的一点P$,再沿截面$A_1BCD_1爬行到点D_1$,则整个过程中蚂蚁爬行的最短路程为( )
A.2
B.$\frac{\sqrt{2}+\sqrt{6}}{2}$
C.$2+\sqrt{2}$
D.$\sqrt{2+\sqrt{2}}$

A.2
B.$\frac{\sqrt{2}+\sqrt{6}}{2}$
C.$2+\sqrt{2}$
D.$\sqrt{2+\sqrt{2}}$
答案:
D解析:如图,连接$AD_{1}$,则$AD_{1}$就是整个过程中蚂蚁爬行的最短路程,过点$D_{1}$作$D_{1}E\perp AA_{1}$交$AA_{1}$的延长线于点E,则$\angle EA_{1}D_{1}=180° - 90° - 45° = 45°=\angle ED_{1}A_{1}$,即$EA_{1}=D_{1}E$。设$EA_{1}=D_{1}E=x$,由勾股定理得$x^{2}+x^{2}=1^{2}$,$x=\frac{\sqrt{2}}{2}$,即$AE=1+\frac{\sqrt{2}}{2}$,$ED_{1}=\frac{\sqrt{2}}{2}$。在$Rt\triangle EAD_{1}$中,由勾股定理得$AD_{1}=\sqrt{(1+\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}}=\sqrt{2+\sqrt{2}}$。故选D。


D解析:如图,连接$AD_{1}$,则$AD_{1}$就是整个过程中蚂蚁爬行的最短路程,过点$D_{1}$作$D_{1}E\perp AA_{1}$交$AA_{1}$的延长线于点E,则$\angle EA_{1}D_{1}=180° - 90° - 45° = 45°=\angle ED_{1}A_{1}$,即$EA_{1}=D_{1}E$。设$EA_{1}=D_{1}E=x$,由勾股定理得$x^{2}+x^{2}=1^{2}$,$x=\frac{\sqrt{2}}{2}$,即$AE=1+\frac{\sqrt{2}}{2}$,$ED_{1}=\frac{\sqrt{2}}{2}$。在$Rt\triangle EAD_{1}$中,由勾股定理得$AD_{1}=\sqrt{(1+\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}}=\sqrt{2+\sqrt{2}}$。故选D。


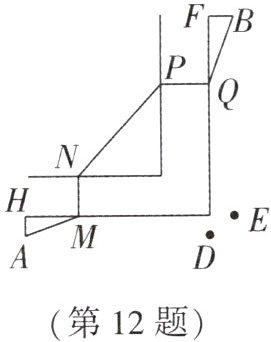
12. (襄阳自主招生)如图,有一条直角弯道河流,河宽为 2,$A$,$B$两地到河岸边的距离均为 1,$AH = BF = 1$,$AD = 7$,$BE = 9$,现欲在河道上架两座桥$MN$,$PQ$,使$AM + MN + NP + PQ + QB$最小,则最小值为(
A.$\sqrt{130}$
B.$\sqrt{145}+2$
C.14
D.12
C
)
A.$\sqrt{130}$
B.$\sqrt{145}+2$
C.14
D.12
答案:
C 解析:如图,延长AH到点J,使得$AJ = MN = 2$,延长BF到点K,使得$BK = PQ = 2$,连接JK交河道于点$N'$,$P'$,得到两座桥$N'M'$,$P'Q'$,此时$AM'+M'N'+N'P'+P'Q'+BQ'$的值最小。延长AH交BK的延长线于点W;在$Rt\triangle JWK$中,$WK = 6$,$WJ = 8$,$\therefore JK=\sqrt{KW^{2}+WJ^{2}}=\sqrt{6^{2}+8^{2}} = 10$,$\therefore AM'+M'N'+N'P'+P'Q'+BQ'=JN'+2+N'P'+2+P'K=4+JK = 14$,$\therefore AM+MN+NP+PQ+QB$的最小值为14。故选C。
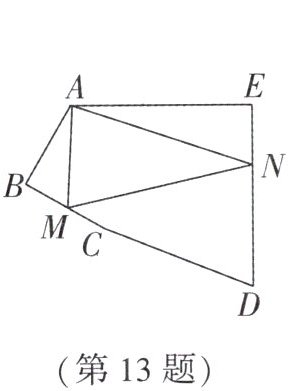
13. (浙江自主招生)如图,五边形$ABCDE$中,$\angle BAE = 120^{\circ}$,$\angle B = \angle E = 90^{\circ}$,$AB = BC = 1$,$AE = DE = 2$,在$BC$,$DE上分别找一点M$,$N$,使$\triangle AMN$的周长最小,则$\triangle AMN$的周长最小值为( )
A.$2\sqrt{6}$
B.$2\sqrt{7}$
C.$4\sqrt{2}$
D.5

A.$2\sqrt{6}$
B.$2\sqrt{7}$
C.$4\sqrt{2}$
D.5
答案:
B 解析:方法一:如图①,作点A关于BC和ED的对称点$A'$,$A''$,连接$A'A''$,交BC于点M,交ED于点N,则$A'A''$即为$\triangle AMN$的周长最小值。过点$A'$作EA延长线的垂线,垂足为H,以点A为原点建立平面直角坐标系,$\because \angle EAB = 120°$,$\therefore \angle A'AH = 60°$。$\because A'H\perp HA$,$\therefore \angle AA'H = 30°$。$\because AB = BC = 1$,$AE = DE = 2$,$\therefore AA' = 2BA = 2$,$AA'' = 2AE = 4$,$\therefore AH=\frac{1}{2}AA' = 1$,$\therefore A'H=\sqrt{2^{2}-1^{2}}=\sqrt{3}$,$\therefore A'(-1,-\sqrt{3})$,$A''(4,0)$。设直线$A'A''$的表达式为$y = kx + b$,则$\begin{cases}4k + b = 0\\-k + b = -\sqrt{3}\end{cases}$,解得$\begin{cases}k = \frac{\sqrt{3}}{5}\\b = -\frac{4\sqrt{3}}{5}\end{cases}$,故$y_{A'A''}=\frac{\sqrt{3}}{5}x-\frac{4\sqrt{3}}{5}$。设直线$AA'$的表达式为$y = ax$,则$-\sqrt{3}=-a$,解得$a = \sqrt{3}$,故直线$AA'$的表达式为$y = \sqrt{3}x$,可得BC所在直线表达式为$y = -\frac{\sqrt{3}}{3}x + d$,同理可得$B(-\frac{1}{2},-\frac{\sqrt{3}}{2})$,则可得$d = -\frac{2\sqrt{3}}{3}$,故直线BC的表达式为$y = -\frac{\sqrt{3}}{3}x-\frac{2\sqrt{3}}{3}$,则$\begin{cases}y = -\frac{\sqrt{3}}{3}x-\frac{2\sqrt{3}}{3}\\y = \frac{\sqrt{3}}{5}x-\frac{4\sqrt{3}}{5}\end{cases}$,解得$\begin{cases}x = -\frac{1}{4}\\y = -\frac{3\sqrt{3}}{4}\end{cases}$,即$M(-\frac{1}{4},-\frac{3\sqrt{3}}{4})$,故$MB=\sqrt{(-\frac{1}{2}+\frac{1}{4})^{2}+(-\frac{\sqrt{3}}{2}+\frac{3\sqrt{3}}{4})^{2}}=\frac{\sqrt{3}}{2}<1$,$\therefore$点M一定在线段BC上。在$Rt\triangle A'H A''$中,$A'H=\sqrt{3}$,$A''H=1 + 4 = 5$,$\therefore A'A''=\sqrt{A'H^{2}+A''H^{2}}=2\sqrt{7}$。故选B。
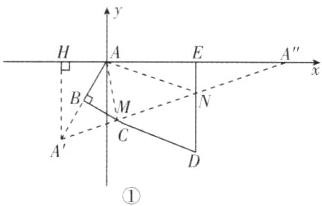
方法二:如图②,过点A作关于BC,ED的对称点$A_{1}$,$A_{2}$,连接$A_{1}M$,$A_{2}N$,$A_{1}A_{2}$,$C_{\triangle AMN}=AM + MN + NA=A_{1}M + MN + A_{2}N\geq A_{1}A_{2}$,当$A_{1}$,$M$,$N$,$A_{2}$共线时,$(A_{1}M + MN + A_{2}N)_{最小}=A_{1}A_{2}$,即$C_{\triangle AMN}$最小,在$\triangle AA_{1}A_{2}$中,$A_{1}A = AB + A_{1}B = 2$,$AA_{2}=4$,作$A_{1}F\perp A_{2}A$,交$A_{2}A$延长线于点F,$\because \angle A_{1}AA_{2}=120°$,$\therefore \angle A_{1}AF = 60°$,$\therefore AF = 1$,$A_{1}F=\sqrt{3}$,而$A_{2}A = 4$,$\therefore A_{2}F = 5$,$\therefore A_{1}A_{2}=\sqrt{A_{2}F^{2}+A_{1}F^{2}}=\sqrt{5^{2}+(\sqrt{3})^{2}}=2\sqrt{7}$。故选B。
B 解析:方法一:如图①,作点A关于BC和ED的对称点$A'$,$A''$,连接$A'A''$,交BC于点M,交ED于点N,则$A'A''$即为$\triangle AMN$的周长最小值。过点$A'$作EA延长线的垂线,垂足为H,以点A为原点建立平面直角坐标系,$\because \angle EAB = 120°$,$\therefore \angle A'AH = 60°$。$\because A'H\perp HA$,$\therefore \angle AA'H = 30°$。$\because AB = BC = 1$,$AE = DE = 2$,$\therefore AA' = 2BA = 2$,$AA'' = 2AE = 4$,$\therefore AH=\frac{1}{2}AA' = 1$,$\therefore A'H=\sqrt{2^{2}-1^{2}}=\sqrt{3}$,$\therefore A'(-1,-\sqrt{3})$,$A''(4,0)$。设直线$A'A''$的表达式为$y = kx + b$,则$\begin{cases}4k + b = 0\\-k + b = -\sqrt{3}\end{cases}$,解得$\begin{cases}k = \frac{\sqrt{3}}{5}\\b = -\frac{4\sqrt{3}}{5}\end{cases}$,故$y_{A'A''}=\frac{\sqrt{3}}{5}x-\frac{4\sqrt{3}}{5}$。设直线$AA'$的表达式为$y = ax$,则$-\sqrt{3}=-a$,解得$a = \sqrt{3}$,故直线$AA'$的表达式为$y = \sqrt{3}x$,可得BC所在直线表达式为$y = -\frac{\sqrt{3}}{3}x + d$,同理可得$B(-\frac{1}{2},-\frac{\sqrt{3}}{2})$,则可得$d = -\frac{2\sqrt{3}}{3}$,故直线BC的表达式为$y = -\frac{\sqrt{3}}{3}x-\frac{2\sqrt{3}}{3}$,则$\begin{cases}y = -\frac{\sqrt{3}}{3}x-\frac{2\sqrt{3}}{3}\\y = \frac{\sqrt{3}}{5}x-\frac{4\sqrt{3}}{5}\end{cases}$,解得$\begin{cases}x = -\frac{1}{4}\\y = -\frac{3\sqrt{3}}{4}\end{cases}$,即$M(-\frac{1}{4},-\frac{3\sqrt{3}}{4})$,故$MB=\sqrt{(-\frac{1}{2}+\frac{1}{4})^{2}+(-\frac{\sqrt{3}}{2}+\frac{3\sqrt{3}}{4})^{2}}=\frac{\sqrt{3}}{2}<1$,$\therefore$点M一定在线段BC上。在$Rt\triangle A'H A''$中,$A'H=\sqrt{3}$,$A''H=1 + 4 = 5$,$\therefore A'A''=\sqrt{A'H^{2}+A''H^{2}}=2\sqrt{7}$。故选B。

方法二:如图②,过点A作关于BC,ED的对称点$A_{1}$,$A_{2}$,连接$A_{1}M$,$A_{2}N$,$A_{1}A_{2}$,$C_{\triangle AMN}=AM + MN + NA=A_{1}M + MN + A_{2}N\geq A_{1}A_{2}$,当$A_{1}$,$M$,$N$,$A_{2}$共线时,$(A_{1}M + MN + A_{2}N)_{最小}=A_{1}A_{2}$,即$C_{\triangle AMN}$最小,在$\triangle AA_{1}A_{2}$中,$A_{1}A = AB + A_{1}B = 2$,$AA_{2}=4$,作$A_{1}F\perp A_{2}A$,交$A_{2}A$延长线于点F,$\because \angle A_{1}AA_{2}=120°$,$\therefore \angle A_{1}AF = 60°$,$\therefore AF = 1$,$A_{1}F=\sqrt{3}$,而$A_{2}A = 4$,$\therefore A_{2}F = 5$,$\therefore A_{1}A_{2}=\sqrt{A_{2}F^{2}+A_{1}F^{2}}=\sqrt{5^{2}+(\sqrt{3})^{2}}=2\sqrt{7}$。故选B。
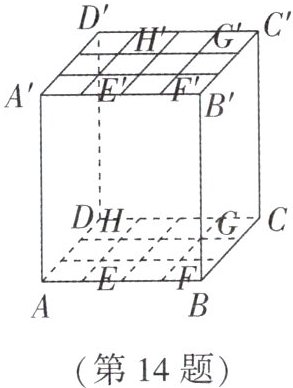
14. (浙江自主招生)如图,$ABCD - A'B'C'D'$为长方体,$AA' = 50cm$,$AB = 40cm$,$AD = 30cm$,把上、下底面都等分成$3×4$个小正方形,其边长均为$10cm$,得到点$E$,$F$,$G$,$H和E'$,$F'$,$G'$,$H'$,假设一只蚂蚁每秒爬行$2cm$,则它从下底面$E点沿表面爬行至上底面G'$点至少要花______秒。

答案:
$10\sqrt{17}$ 解析:由图①有$EG'=\sqrt{20^{2}+80^{2}}=20\sqrt{17}$(cm),由图②有$EG'=\sqrt{10^{2}+90^{2}}=10\sqrt{82}$(cm),$10\sqrt{82}>20\sqrt{17}$,故最短时间为$20\sqrt{17}÷2 = 10\sqrt{17}$(秒)。故答案为$10\sqrt{17}$。


$10\sqrt{17}$ 解析:由图①有$EG'=\sqrt{20^{2}+80^{2}}=20\sqrt{17}$(cm),由图②有$EG'=\sqrt{10^{2}+90^{2}}=10\sqrt{82}$(cm),$10\sqrt{82}>20\sqrt{17}$,故最短时间为$20\sqrt{17}÷2 = 10\sqrt{17}$(秒)。故答案为$10\sqrt{17}$。


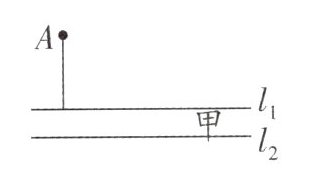
15. (全国初中数学竞赛)如图,五羊大学建立分校,校本部与分校隔着两条平行的小河,$l_1// l_2$表示小河甲,$l_3// l_4$表示小河乙,$A$为校本部大门,$B$为分校大门,为方便人员来往,要在两条小河上各建一座桥,桥面垂直于河岸。图中的尺寸是:甲河宽 8 米,乙河宽 10 米,$A$到甲河垂直距离为 40 米,$B$到乙河垂直距离为 20 米,两河距离 100 米,$A$,$B$两点水平距离(与小河平行方向)120 米,为使$A$,$B$两点间来往路程最短,两座桥都按这个目标而建,那么,此时$A$,$B$两点间来往的路程是多少米?
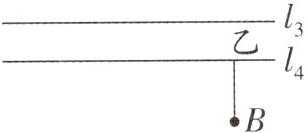


答案:
如图,作$AA'\perp l_{1}$,且$AA' = 8$米,作$BB'\perp l_{4}$,且$BB' = 10$米,连接$A'B'$交$l_{2}$,$l_{3}$于点D,E,过点D作$DC\perp l_{1}$,垂足为C;过点E作$EF\perp l_{4}$,垂足为F,连接AC,BF。$\because AA' = CD = 8$米,$AA'\perp l_{1}$,$DC\perp l_{1}$,$\therefore AA' = CD$,$AA'// CD$,$\therefore$四边形$AA'DC$是平行四边形,$\therefore AC = A'D$。同理可得,$BF = B'E$,$\therefore AC + CD + DE + EF + BF=AA'+A'B'+BB'=8 + 10 + A'B'=18+\sqrt{120^{2}+(40 + 20 + 100)^{2}}=18 + 200 = 218$(米)。答:A,B两点间来往的路程是218米。

如图,作$AA'\perp l_{1}$,且$AA' = 8$米,作$BB'\perp l_{4}$,且$BB' = 10$米,连接$A'B'$交$l_{2}$,$l_{3}$于点D,E,过点D作$DC\perp l_{1}$,垂足为C;过点E作$EF\perp l_{4}$,垂足为F,连接AC,BF。$\because AA' = CD = 8$米,$AA'\perp l_{1}$,$DC\perp l_{1}$,$\therefore AA' = CD$,$AA'// CD$,$\therefore$四边形$AA'DC$是平行四边形,$\therefore AC = A'D$。同理可得,$BF = B'E$,$\therefore AC + CD + DE + EF + BF=AA'+A'B'+BB'=8 + 10 + A'B'=18+\sqrt{120^{2}+(40 + 20 + 100)^{2}}=18 + 200 = 218$(米)。答:A,B两点间来往的路程是218米。

查看更多完整答案,请扫码查看


