第106页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
8 (鄂州中考)已知菱形纸片 $ABCD$ 的边长为 $8$,$\angle A = 60^{\circ}$,$E$ 为 $AB$ 边上的点,过点 $E$ 作 $EF // BD$ 交 $AD$ 于点 $F$。将菱形先沿 $EF$ 按图①所示方式折叠,点 $A$ 落在点 $A'$ 处,过点 $A'$ 作 $GH // BD$ 分别交线段 $BC$,$DC$ 于点 $G$,$H$,再将菱形沿 $GH$ 按图①所示方式折叠,点 $C$ 落在点 $C'$ 处,$C'G$ 与 $C'H$ 分别交 $A'E$,$A'F$ 于点 $M$,$N$。若点 $C'$ 在 $\triangle A'EF$ 的内部或边上,则我们称四边形 $A'MC'N$(即图中阴影部分)为“重叠四边形”。
(1)若把菱形纸片 $ABCD$ 放在菱形网格中(图中每个小三角形都是边长为 $1$ 的等边三角形),点 $A$,$B$,$C$,$D$,$E$ 恰好落在网格图中的格点上,如图②所示,请直接写出此时重叠四边形 $A'MC'N$ 的面积;
(2)实验探究:设 $AE$ 的长为 $m$,若重叠四边形 $A'MC'N$ 存在,试用含 $m$ 的代数式表示重叠四边形 $A'MC'N$ 的面积,并写出 $m$ 的取值范围(直接写出结果,备用图供实验探究使用)。
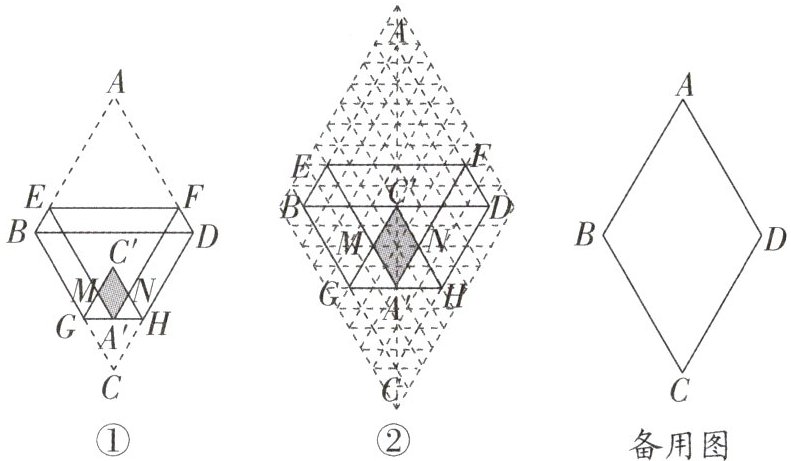
(1)若把菱形纸片 $ABCD$ 放在菱形网格中(图中每个小三角形都是边长为 $1$ 的等边三角形),点 $A$,$B$,$C$,$D$,$E$ 恰好落在网格图中的格点上,如图②所示,请直接写出此时重叠四边形 $A'MC'N$ 的面积;
(2)实验探究:设 $AE$ 的长为 $m$,若重叠四边形 $A'MC'N$ 存在,试用含 $m$ 的代数式表示重叠四边形 $A'MC'N$ 的面积,并写出 $m$ 的取值范围(直接写出结果,备用图供实验探究使用)。

答案:
(1)
∵菱形纸片ABCD的边长为8,∠A = 60°,
∴AB = BC = AD = CD = 8,∠ABC = ∠ADC = 180° - 60° = 120°,AB//CD,AD//BC.根据题意得∠MA'N = ∠C' = 60°.把菱形纸片ABCD放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A,B,C,D,E恰好落在网格图中的格点上,
∴∠ABD = ∠AEF = 60°,根据折叠可知,∠FEA' = ∠AEF = 60°,
∴∠AEA' = 60° + 60° = 120°,∠ABC = 60° + 60° = 120°,
∴∠AEA' = ∠ABC = 120°,
∴A'E//BC,同理可得A'F//AB,C'H//AD,C'G//AB,
∴A'N//CM,A'M//C'N,
∴四边形A'MC'N是平行四边形,同理可得四边形EBGM、DFNH为平行四边形,
∴EM = BG,NF = HD.
∵GH//BD,
∴∠CGH = ∠CBD = 60°,∠CHG = ∠CDB = 60°,
∴∠CGH = ∠CHG,
∴CG = CH.
∵CB = CD,
∴GB = HD,
∴EM = NF.
∵A'E = A'F,
∴A'M = A'N,
∴四边形A'MC'N是菱形.根据题意可知,AE = 6,AB = 8,根据折叠可知,A'E = AE = 6,CG = BG = $\frac{1}{2}$BC = 4,
∴EM = BG = 4,
∴A'M = 6 - 4 = 2.
∵∠MA'N = 60°,A'M = A'N,
∴△A'MN为等边三角形,
∴MN = 2,A'C' = 2$\sqrt{3}$,
∴重叠四边形A'MC'N的面积为$\frac{1}{2}$MN·A'C' = $\frac{1}{2}$×2×2$\sqrt{3}$ = 2$\sqrt{3}$.
(2)$S_{四边形A'MC'N}=\frac{\sqrt{3}}{2}$(8 - m)²,$\frac{16}{3}$≤m<8 解析:根据
(1)可知,四边形A'MC'N为菱形,四边形GMEB为平行四边形.
∵四边形GMEB为平行四边形,
∴GM = BE = 8 - m.
∵四边形A'MC'N为菱形,∠EA'F = ∠C' = 60°,
∴A'M//C'H,
∴∠A'MG = ∠C' = 60°.
∵BE//GM,
∴∠CGC' = ∠ABC = 120°.根据
(1)可知,△CGH为等边三角形,
∴∠CGH = 60°,
∴∠A'GM = 120° - 60° = 60°,
∴△A'GM是等边三角形,
∴A'M = GM = 8 - m.根据
(1)可得MN = A'M = 8 - m,A'C' = $\sqrt{3}$(8 - m),
∴用含m的代数式表示重叠四边形A'MC'N的面积为$\frac{\sqrt{3}}{2}$(8 - m)².如图,连接AC,BD.
∵EF//BD,
∴∠AEF = ∠ABD = 60°,∠AFE = ∠ADB = 60°,
∴∠A'EF = ∠AEF = 60°,
∴∠BEA' = 180° - 60° - 60° = 60°,
∴∠BEA' = ∠BAD,
∴A'E //AD,同理可得A'F//AB,
∴四边形AEA'F为菱形.
∵∠BAD = ∠AEF = 60°,
∴△AEF为等边三角形,
∴AE = AF = EF = m,
∴四边形AEA'F为菱形,
∴AA'⊥EF,AO' = A'O',EO' = FO' = $\frac{1}{2}$m,
∴$AO' = \sqrt{AE^{2}-EO'^{2}}=\frac{\sqrt{3}}{2}$m,
∴AA' = 2AO' = $\sqrt{3}$m.
∵菱形ABCD的边长为8,∠BAD = 60°,
∴同理可得,BD = 8,AC = 8$\sqrt{3}$,
∴CA' = 8$\sqrt{3}$ - $\sqrt{3}$m.
∵点C'在△A'EF的内部或边上,
∴$\begin{cases}8\sqrt{3}-\sqrt{3}m\leqslant\frac{\sqrt{3}}{2}m\\8 - m>0\end{cases}$,解得$\frac{16}{3}$≤m<8,
∴m的取值范围为$\frac{16}{3}$≤m<8.
(1)
∵菱形纸片ABCD的边长为8,∠A = 60°,
∴AB = BC = AD = CD = 8,∠ABC = ∠ADC = 180° - 60° = 120°,AB//CD,AD//BC.根据题意得∠MA'N = ∠C' = 60°.把菱形纸片ABCD放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A,B,C,D,E恰好落在网格图中的格点上,
∴∠ABD = ∠AEF = 60°,根据折叠可知,∠FEA' = ∠AEF = 60°,
∴∠AEA' = 60° + 60° = 120°,∠ABC = 60° + 60° = 120°,
∴∠AEA' = ∠ABC = 120°,
∴A'E//BC,同理可得A'F//AB,C'H//AD,C'G//AB,
∴A'N//CM,A'M//C'N,
∴四边形A'MC'N是平行四边形,同理可得四边形EBGM、DFNH为平行四边形,
∴EM = BG,NF = HD.
∵GH//BD,
∴∠CGH = ∠CBD = 60°,∠CHG = ∠CDB = 60°,
∴∠CGH = ∠CHG,
∴CG = CH.
∵CB = CD,
∴GB = HD,
∴EM = NF.
∵A'E = A'F,
∴A'M = A'N,
∴四边形A'MC'N是菱形.根据题意可知,AE = 6,AB = 8,根据折叠可知,A'E = AE = 6,CG = BG = $\frac{1}{2}$BC = 4,
∴EM = BG = 4,
∴A'M = 6 - 4 = 2.
∵∠MA'N = 60°,A'M = A'N,
∴△A'MN为等边三角形,
∴MN = 2,A'C' = 2$\sqrt{3}$,
∴重叠四边形A'MC'N的面积为$\frac{1}{2}$MN·A'C' = $\frac{1}{2}$×2×2$\sqrt{3}$ = 2$\sqrt{3}$.
(2)$S_{四边形A'MC'N}=\frac{\sqrt{3}}{2}$(8 - m)²,$\frac{16}{3}$≤m<8 解析:根据
(1)可知,四边形A'MC'N为菱形,四边形GMEB为平行四边形.
∵四边形GMEB为平行四边形,
∴GM = BE = 8 - m.
∵四边形A'MC'N为菱形,∠EA'F = ∠C' = 60°,
∴A'M//C'H,
∴∠A'MG = ∠C' = 60°.
∵BE//GM,
∴∠CGC' = ∠ABC = 120°.根据
(1)可知,△CGH为等边三角形,
∴∠CGH = 60°,
∴∠A'GM = 120° - 60° = 60°,
∴△A'GM是等边三角形,
∴A'M = GM = 8 - m.根据
(1)可得MN = A'M = 8 - m,A'C' = $\sqrt{3}$(8 - m),
∴用含m的代数式表示重叠四边形A'MC'N的面积为$\frac{\sqrt{3}}{2}$(8 - m)².如图,连接AC,BD.
∵EF//BD,
∴∠AEF = ∠ABD = 60°,∠AFE = ∠ADB = 60°,
∴∠A'EF = ∠AEF = 60°,
∴∠BEA' = 180° - 60° - 60° = 60°,
∴∠BEA' = ∠BAD,
∴A'E //AD,同理可得A'F//AB,
∴四边形AEA'F为菱形.
∵∠BAD = ∠AEF = 60°,
∴△AEF为等边三角形,
∴AE = AF = EF = m,
∴四边形AEA'F为菱形,
∴AA'⊥EF,AO' = A'O',EO' = FO' = $\frac{1}{2}$m,
∴$AO' = \sqrt{AE^{2}-EO'^{2}}=\frac{\sqrt{3}}{2}$m,
∴AA' = 2AO' = $\sqrt{3}$m.
∵菱形ABCD的边长为8,∠BAD = 60°,
∴同理可得,BD = 8,AC = 8$\sqrt{3}$,
∴CA' = 8$\sqrt{3}$ - $\sqrt{3}$m.
∵点C'在△A'EF的内部或边上,
∴$\begin{cases}8\sqrt{3}-\sqrt{3}m\leqslant\frac{\sqrt{3}}{2}m\\8 - m>0\end{cases}$,解得$\frac{16}{3}$≤m<8,
∴m的取值范围为$\frac{16}{3}$≤m<8.
9 (重庆自主招生)如图,在菱形 $ABCD$ 中,对角线 $AC$ 与 $BD$ 交于点 $O$,$CE \perp AB$ 于点 $E$,$F$ 为线段 $AE$ 上一点,若 $AC = 6$,$BD = 8$,$AF = \frac{4}{9}AE$,则线段 $CF$ 的长度为(

A.$\frac{7}{5}$
B.$\frac{13}{5}$
C.$\frac{14}{5}$
D.$\frac{26}{5}$
D
)
A.$\frac{7}{5}$
B.$\frac{13}{5}$
C.$\frac{14}{5}$
D.$\frac{26}{5}$
答案:
D
10 (全国初中数学竞赛)如图是以 $KL$ 所在的直线为对称轴的轴对称图形,六边形 $EFGHLK$ 的各个内角相等,记四边形 $HCH'L$、四边形 $EKE'A$、$\triangle BGF$ 的周长分别为 $C_1$,$C_2$,$C_3$,且 $C_1 = 2C_2 = 4C_3$,已知 $FG = LK$,$EF = 6$,则 $AB$ 的长是(
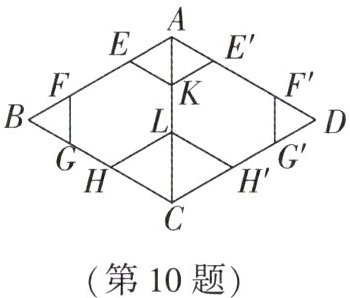
A.$9.5$
B.$10$
C.$10.5$
D.$11$
D
)
A.$9.5$
B.$10$
C.$10.5$
D.$11$
答案:
D
11 如图,在梯形 $ABCD$ 中,$AB // CD$,$AD = BC = CD = 2$,$\angle B = 60^{\circ}$,$M$,$N$,$E$,$F$ 分别是四边中点,则四边形 $MENF$ 的周长为

4$\sqrt{3}$
。
答案:
4$\sqrt{3}$
12 如图,在凸五边形 $ABCDE$ 中,$\angle A = \angle B = 120^{\circ}$,$EA = AB = BC = 2$,$CD = DE = 4$,则它的面积为

7$\sqrt{3}$
。
答案:
7$\sqrt{3}$ 解析:如图,延长EA,CB相交于点F,作CG⊥EF于点G,作BH⊥EF于点H.因为∠EAB = ∠CBA = 120°,所以∠FAB = ∠FBA = 60°,所以△FAB为等边三角形,AF = FB = AB = 2,所以CD = DE = EF = FC = 4,所以四边形EFCD是菱形,所以$S_{五边形ABCDE}=S_{四边形CDEF}-S_{\triangle ABF}=EF\cdot CG-\frac{1}{2}FA\cdot BH=EF\cdot\frac{\sqrt{3}}{2}FC-\frac{1}{2}FA\cdot\frac{\sqrt{3}}{2}FB=8\sqrt{3}-\sqrt{3}=7\sqrt{3}$.
13 (重庆自主招生)如图,在平面直角坐标系内放置一菱形 $OABC$,已知 $\angle ABC = 60^{\circ}$,$OA = 2$。先将菱形 $OABC$ 沿 $x$ 轴的正方向无滑动旋转,每次旋转 $60^{\circ}$,连续旋转 $999$ 次,点 $B$ 的落点依次为 $B_1$,$B_2$,$B_3$,…$$,则点 $B_{999}$ 的坐标为

(1332,0)
。
答案:
(1332,0) 解析:如图,连接AC.
∵四边形OABC是菱形,
∴OA = AB = BC = OC.
∵∠ABC = 60°,
∴△ABC是等边三角形,
∴AC = AB.
∴AC = OA.
∵OA = 2,
∴AC = 2.画出第5次、第6次、第7次翻转后的图形. 由图可知每翻转6次,图形向右平移4个边长.
∵999 = 166×6 + 3,
∴点B向右平移1328(即166×4×2)到点$B_{996}$.
∵点$B_{996}$的坐标为(1328,2$\sqrt{3}$),
∴点$B_{999}$的坐标为(1332,0).
∵四边形OABC是菱形,
∴OA = AB = BC = OC.
∵∠ABC = 60°,
∴△ABC是等边三角形,
∴AC = AB.
∴AC = OA.
∵OA = 2,
∴AC = 2.画出第5次、第6次、第7次翻转后的图形. 由图可知每翻转6次,图形向右平移4个边长.
∵999 = 166×6 + 3,
∴点B向右平移1328(即166×4×2)到点$B_{996}$.
∵点$B_{996}$的坐标为(1328,2$\sqrt{3}$),
∴点$B_{999}$的坐标为(1332,0).
查看更多完整答案,请扫码查看


