第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
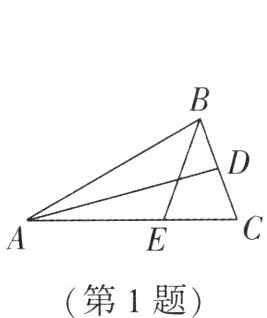
1. 如图,$ AD $ 与 $ BE $ 是 $ \triangle ABC $ 的角平分线,$ D $,$ E $ 分别在 $ BC $,$ AC $ 上,若 $ AD = AB $,$ BE = BC $,则 $ \angle C = $
A.$ 69° $
B.$ \left( \frac{623}{9} \right)° $
C.$ \left( \frac{900}{13} \right)° $
D.不能确定
C
[img]
A.$ 69° $
B.$ \left( \frac{623}{9} \right)° $
C.$ \left( \frac{900}{13} \right)° $
D.不能确定
答案:
C
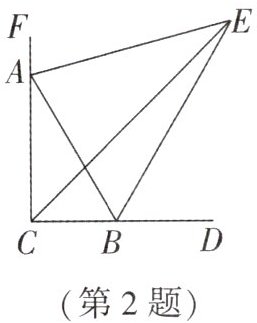
2. 如图,在 $ Rt \triangle ABC $ 中,$ \angle ACB = 90° $,$ \angle BAC = 30° $,$ \angle ACB $ 的平分线与 $ \triangle ABC $ 的外角 $ \angle ABD $ 的平分线交于点 $ E $,则 $ \angle AEB $ 是[
A.$ 50° $
B.$ 45° $
C.$ 40° $
D.$ 35° $
B
]
A.$ 50° $
B.$ 45° $
C.$ 40° $
D.$ 35° $
答案:
B
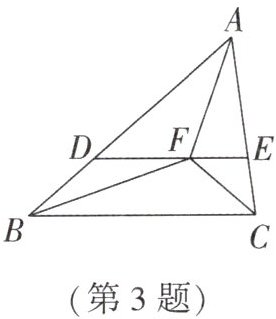
3. 如图,已知 $ \triangle ABC $ 中,$ AB = 6 $,$ BC = 5 $,$ AC = 4 $,$ \angle ABC $,$ \angle ACB $ 的平分线相交于点 $ F $,过点 $ F $ 作 $ DE // BC $,交 $ AB $ 于点 $ D $,交 $ AC $ 于点 $ E $,连接 $ AF $,则下列结论:
① $ DE = BD + CE $;
② $ \angle BFC = 90° + \frac{1}{2} \angle ABC $;
③ $ \triangle ADE $ 的周长为 $ 10 $;
④ $ S_{\triangle ABF} : S_{\triangle ACF} : S_{\triangle BCF} = 6 : 4 : 5 $。
正确的是
A.①③④
B.①②③
C.①②③④
D.②③④
① $ DE = BD + CE $;
② $ \angle BFC = 90° + \frac{1}{2} \angle ABC $;
③ $ \triangle ADE $ 的周长为 $ 10 $;
④ $ S_{\triangle ABF} : S_{\triangle ACF} : S_{\triangle BCF} = 6 : 4 : 5 $。
正确的是
A

A.①③④
B.①②③
C.①②③④
D.②③④
答案:
A
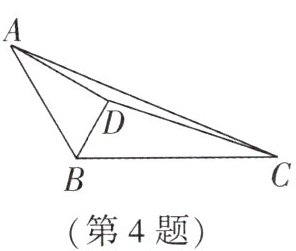
4. 如图,在 $ \triangle ABC $ 中,$ BD $ 平分 $ \angle ABC $,$ AD $ 垂直于 $ BD $,$ \triangle BCD $ 的面积为 $ 45 $,$ \triangle ADC $ 的面积为 $ 20 $,则三角形 $ ABD $ 的面积等于
25
。 [img]
答案:
25
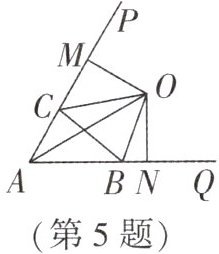
5. 如图,$ CO $,$ BO $ 是 $ \triangle ABC $ 的两个外角 $ \angle PCB $,$ \angle QBC $ 的平分线,$ OM \perp AP $,$ ON \perp AQ $,且 $ OM = ON $。下列结论中正确的有
① $ \angle PAO = \angle QAO $;
② $ \angle AOB = \frac{1}{2} \angle ACB $;
③ $ 2 \angle COB = 180° + \angle CAB $;
④ $ \angle PAQ + 2 \angle COB = 180° $。
[img]
3
个。① $ \angle PAO = \angle QAO $;
② $ \angle AOB = \frac{1}{2} \angle ACB $;
③ $ 2 \angle COB = 180° + \angle CAB $;
④ $ \angle PAQ + 2 \angle COB = 180° $。
[img]

答案:
3
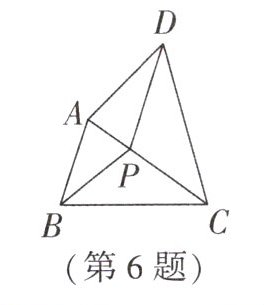
6. (宣城自主招生)如图,四边形 $ ABCD $ 中,$ \angle A $,$ \angle B $,$ \angle C $,$ \angle D $ 的平分线恰相交于一点 $ P $($ A $,$ P $,$ C $ 三点不共线),记 $ \triangle APD $,$ \triangle APB $,$ \triangle BPC $,$ \triangle DPC $ 的面积分别为 $ S_1 $,$ S_2 $,$ S_3 $,$ S_4 $,则有
A.$ S_1 + S_3 = S_2 + S_4 $
B.$ S_1 + S_2 = S_3 + S_4 $
C.$ S_1 + S_4 = S_2 + S_3 $
D.$ S_1 = S_3 $
$S_1+S_3=S_2+S_4$
[img]
A.$ S_1 + S_3 = S_2 + S_4 $
B.$ S_1 + S_2 = S_3 + S_4 $
C.$ S_1 + S_4 = S_2 + S_3 $
D.$ S_1 = S_3 $
答案:
A 解析:四边形ABCD,四个内角的平分线交于一点P,则P到该四边形每条边的距离相等,如图,可将四边形分成8个等高的三角形,面积分别是a,a,b,b,c,c,d,d,则S₁=a+d,S₂=a+b,S₃=b+c,S₄=c+d,
∴S₁+S₃=a+b+c+d=S₂+S₄.故选A.
∴S₁+S₃=a+b+c+d=S₂+S₄.故选A.
7. 如图,正三角形 $ ABC $ 和正三角形 $ CDE $ 中,$ B $,$ C $,$ D $ 三点共线,且 $ BC = 3CD $,连接 $ AD $ 和 $ BE $ 相交于点 $ F $,连接 $ FC $,以下结论中不正确的是
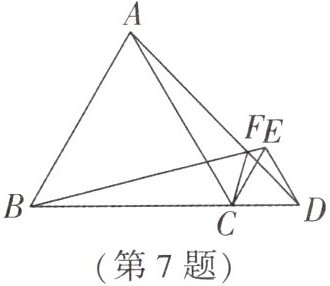
A.$ AD = BE $
B.$ FC $ 平分 $ \angle BFD $
C.$ BF = 2CF $
D.$ \angle AFB = 60° $
C
[img]
A.$ AD = BE $
B.$ FC $ 平分 $ \angle BFD $
C.$ BF = 2CF $
D.$ \angle AFB = 60° $
答案:
C 解析:
∵△ABC和△CDE都是正三角形,
∴CA=CB,∠ACB=60°,CD=CE,∠DCE=60°.
∵B,C,D三点共线,
∴∠ACE=180°−∠ACB−∠DCE=180°−60°−60°=60°,
∴∠ACD=∠ACE+∠DCE=60°+60°=120°,∠BCE=∠ACE+∠ACB=60°+60°=120°,
∴∠ACD=∠BCE.在△ACD和△BCE中,{AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE,故A选项正确,不符合题意;
∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠ACB是△ACD的外角,
∴∠CAD+∠ADC=∠ACB=60°.
∵∠AFB是△BFD的外角,
∴∠AFB=∠FBD+∠FDB=∠CAD+∠ADC=60°,故D选项正确,不符合题意;如图,过点C作CG⊥AD于点G,CH⊥BE于点H,
∵△ACD≌△BCE,
∴CG=CH,
∴FC平分∠BFD,故B选项正确,不符合题意;如图,过点F作FM⊥BD于M,
∵S△BCF=$\frac{1}{2}$BC·FM,S△DCF=$\frac{1}{2}$CD·FM,BC=3CD,
∴S△BCF=3S△DCF.
∵S△BCF=$\frac{1}{2}$BF·CH,S△DCF=$\frac{1}{2}$DF·CG,
∴BF·CH=3DF·CG.
∵CG=CH,
∴BF=3DF.
∵∠AFB=60°,FC平分∠BFD,
∴∠BFC=60°.仅当FC⊥BC时,BF=2CF;而当FC⊥BC时,△FCD为有一个角为60°的直角三角形,此时DF=2CF,故DF=BF,与BF=3DF矛盾,故FC⊥BC不成立,即BF=2CF不成立.故C选项不正确.故选C.
∵△ABC和△CDE都是正三角形,
∴CA=CB,∠ACB=60°,CD=CE,∠DCE=60°.
∵B,C,D三点共线,
∴∠ACE=180°−∠ACB−∠DCE=180°−60°−60°=60°,
∴∠ACD=∠ACE+∠DCE=60°+60°=120°,∠BCE=∠ACE+∠ACB=60°+60°=120°,
∴∠ACD=∠BCE.在△ACD和△BCE中,{AC=BC,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE,故A选项正确,不符合题意;
∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠ACB是△ACD的外角,
∴∠CAD+∠ADC=∠ACB=60°.
∵∠AFB是△BFD的外角,
∴∠AFB=∠FBD+∠FDB=∠CAD+∠ADC=60°,故D选项正确,不符合题意;如图,过点C作CG⊥AD于点G,CH⊥BE于点H,
∵△ACD≌△BCE,
∴CG=CH,
∴FC平分∠BFD,故B选项正确,不符合题意;如图,过点F作FM⊥BD于M,
∵S△BCF=$\frac{1}{2}$BC·FM,S△DCF=$\frac{1}{2}$CD·FM,BC=3CD,
∴S△BCF=3S△DCF.
∵S△BCF=$\frac{1}{2}$BF·CH,S△DCF=$\frac{1}{2}$DF·CG,
∴BF·CH=3DF·CG.
∵CG=CH,
∴BF=3DF.
∵∠AFB=60°,FC平分∠BFD,
∴∠BFC=60°.仅当FC⊥BC时,BF=2CF;而当FC⊥BC时,△FCD为有一个角为60°的直角三角形,此时DF=2CF,故DF=BF,与BF=3DF矛盾,故FC⊥BC不成立,即BF=2CF不成立.故C选项不正确.故选C.
8. (成都自主招生)在 $ \triangle ABC $ 中,$ \angle C = 90° $,$ BC = a $,$ CA = b $,$ AB = c $,两条内角平分线 $ AE $,$ BF $ 交于点 $ O $。若 $ \triangle OEF $ 和 $ \triangle OAB $ 的面积分别为 $ S_{\triangle OEF} $ 和 $ S_{\triangle OAB} $,则 $ \frac{S_{\triangle OEF}}{S_{\triangle OAB}} = $
A.$ \frac{a + b - c}{a + b + c} $
B.$ \frac{a + b - c}{a + b + 2c} $
C.$ \frac{2c - a - b}{a + b + c} $
D.$ \frac{2c - a - b}{a + b + 2c} $
$\frac{ab}{ab+ac+bc}$
A.$ \frac{a + b - c}{a + b + c} $
B.$ \frac{a + b - c}{a + b + 2c} $
C.$ \frac{2c - a - b}{a + b + c} $
D.$ \frac{2c - a - b}{a + b + 2c} $
答案:
A 解析:如图①,S△OAB=S△ABC−S△ACE−S△BCF+S△OEF+S△CEF=$\frac{1}{2}$ab−$\frac{1}{2}$b·CE−$\frac{1}{2}$a·CF+S△OEF+$\frac{1}{2}$CE·CF=$\frac{1}{2}$(a−CE)(b−CF)+S△OEF=$\frac{1}{2}$BE·AF+S△OEF,从而$\frac{S_{\triangle OEF}}{S_{\triangle OAB}}=1-\frac{\frac{1}{2}BE\cdot AF}{S_{\triangle OAB}}$.如图②,作OK,OL,OM分别垂直于BC,AC,AB,连接OC.由角平分线的性质,得OK=OL=OM.设OK=r,S△OAB=$\frac{1}{2}$cr.由于OK=OL,∠OKC=∠KCL=∠CLO=90°,故四边形OKCL是正方形.S△BCF=$\frac{1}{2}$a·CF,S△BOK=$\frac{1}{2}$r(a−r),S梯形OKCF=$\frac{1}{2}$r(r+CF),从而$\frac{1}{2}$a·CF=$\frac{1}{2}$r(a−r)+$\frac{1}{2}$r²+$\frac{1}{2}$r·CF,解得CF=$\frac{ar}{a−r}$,同理可得CE=$\frac{br}{b−r}$,故AF=b−$\frac{ar}{a−r}$=$\frac{ab−r(a+b)}{a−r}$,BE=a−$\frac{br}{b−r}$=$\frac{ab−r(a+b)}{b−r}$.
∵S△ABC=S△OAB+S△OBC+S△OCA=$\frac{1}{2}$cr+$\frac{1}{2}$ar+$\frac{1}{2}$br,
∴r=$\frac{ab}{a+b+c}$,
∴S△OAB=$\frac{abc}{2(a+b+c)}$.
∵AF=$\frac{ab−r(a+b)}{a−r}$=$\frac{ab-\frac{ab(a+b)}{a+b+c}}{a-\frac{ab}{a+b+c}}$=$\frac{bc}{a+c}$,BE=$\frac{ab−r(a+b)}{b−r}$=$\frac{ab-\frac{ab(a+b)}{a+b+c}}{b-\frac{ab}{a+b+c}}$=$\frac{ac}{b+c}$,
∴AF·BE=$\frac{bc}{a+c}$·$\frac{ac}{b+c}$=$\frac{abc^{2}}{(a+c)(b+c)}$,
∴$\frac{S_{\triangle OEF}}{S_{\triangle OAB}}=1-\frac{\frac{abc^{2}}{2(a+c)(b+c)}}{\frac{abc}{2(a+b+c)}}=1-\frac{c(a+b+c)}{(a+c)(b+c)}=\frac{(a+c)(b+c)-c(a+b+c)}{(a+c)(b+c)}=\frac{ab+ac+bc+c^{2}-ac-bc-c^{2}}{(a+c)(b+c)}=\frac{ab}{(a+c)(b+c)}=\frac{ab}{ab+ac+bc+c^{2}}=\frac{ab}{ab+ac+bc+\frac{1}{2}c^{2}+\frac{1}{2}c^{2}}=\frac{ab}{ab+ac+bc+\frac{1}{2}c^{2}+\frac{1}{2}(a^{2}+b^{2})-\frac{a^{2}+b^{2}}{2}+c^{2}}=\frac{ab}{\frac{1}{2}(a+b+c)^{2}-\frac{a^{2}+b^{2}-c^{2}}{2}}=\frac{ab}{\frac{(a+b+c)^{2}-(a^{2}+b^{2}-c^{2})}{2}}=\frac{2ab}{(a+b+c)^{2}-(a^{2}+b^{2}-c^{2})}=\frac{2ab}{2ab + 2ac + 2bc}=\frac{ab}{ab+ac+bc}=\frac{1}{1+\frac{c}{a}+\frac{c}{b}}$.无法继续推导得到选项中的形式,可能原式解析存在复杂步骤省略,最终答案为A.
∵S△ABC=S△OAB+S△OBC+S△OCA=$\frac{1}{2}$cr+$\frac{1}{2}$ar+$\frac{1}{2}$br,
∴r=$\frac{ab}{a+b+c}$,
∴S△OAB=$\frac{abc}{2(a+b+c)}$.
∵AF=$\frac{ab−r(a+b)}{a−r}$=$\frac{ab-\frac{ab(a+b)}{a+b+c}}{a-\frac{ab}{a+b+c}}$=$\frac{bc}{a+c}$,BE=$\frac{ab−r(a+b)}{b−r}$=$\frac{ab-\frac{ab(a+b)}{a+b+c}}{b-\frac{ab}{a+b+c}}$=$\frac{ac}{b+c}$,
∴AF·BE=$\frac{bc}{a+c}$·$\frac{ac}{b+c}$=$\frac{abc^{2}}{(a+c)(b+c)}$,
∴$\frac{S_{\triangle OEF}}{S_{\triangle OAB}}=1-\frac{\frac{abc^{2}}{2(a+c)(b+c)}}{\frac{abc}{2(a+b+c)}}=1-\frac{c(a+b+c)}{(a+c)(b+c)}=\frac{(a+c)(b+c)-c(a+b+c)}{(a+c)(b+c)}=\frac{ab+ac+bc+c^{2}-ac-bc-c^{2}}{(a+c)(b+c)}=\frac{ab}{(a+c)(b+c)}=\frac{ab}{ab+ac+bc+c^{2}}=\frac{ab}{ab+ac+bc+\frac{1}{2}c^{2}+\frac{1}{2}c^{2}}=\frac{ab}{ab+ac+bc+\frac{1}{2}c^{2}+\frac{1}{2}(a^{2}+b^{2})-\frac{a^{2}+b^{2}}{2}+c^{2}}=\frac{ab}{\frac{1}{2}(a+b+c)^{2}-\frac{a^{2}+b^{2}-c^{2}}{2}}=\frac{ab}{\frac{(a+b+c)^{2}-(a^{2}+b^{2}-c^{2})}{2}}=\frac{2ab}{(a+b+c)^{2}-(a^{2}+b^{2}-c^{2})}=\frac{2ab}{2ab + 2ac + 2bc}=\frac{ab}{ab+ac+bc}=\frac{1}{1+\frac{c}{a}+\frac{c}{b}}$.无法继续推导得到选项中的形式,可能原式解析存在复杂步骤省略,最终答案为A.
9. (长沙自主招生)如图,在 $ Rt \triangle ABC $ 中,$ \angle C = 90° $,$ \angle B = 60° $,$ \angle A $ 的平分线 $ AD $ 交 $ BC $ 于点 $ D $,则 $ \frac{AB - AC}{CD} = $
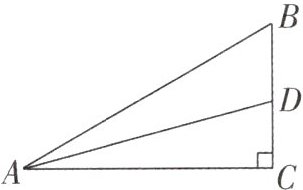
$\frac{\sqrt{3}}{3}$
。 [img]
答案:
$\frac{\sqrt{3}}{3}$ 解析:如图,过点D作DE⊥AB于点E.
∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DE=CD.
∵DE⊥AB,
∴∠BED=90°.
∵∠B=60°,
∴∠BDE=180°−90°−60°=30°,
∴BD=2BE.由勾股定理得DE=CD=$\sqrt{3}$BE,由勾股定理得AE²=AD²−DE²,AC²=AD²−CD²,
∴AE=AC,即AB−AC=AB−AE=BE,
∴$\frac{AB−AC}{CD}=\frac{BE}{\sqrt{3}BE}=\frac{\sqrt{3}}{3}$,故答案为$\frac{\sqrt{3}}{3}$.
∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DE=CD.
∵DE⊥AB,
∴∠BED=90°.
∵∠B=60°,
∴∠BDE=180°−90°−60°=30°,
∴BD=2BE.由勾股定理得DE=CD=$\sqrt{3}$BE,由勾股定理得AE²=AD²−DE²,AC²=AD²−CD²,
∴AE=AC,即AB−AC=AB−AE=BE,
∴$\frac{AB−AC}{CD}=\frac{BE}{\sqrt{3}BE}=\frac{\sqrt{3}}{3}$,故答案为$\frac{\sqrt{3}}{3}$.
查看更多完整答案,请扫码查看


