《2025年学霸题中题八年级数学上册浙教版》

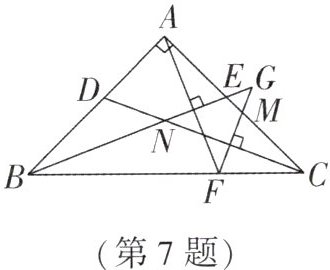
7. 如图,等腰直角三角形 $ABC$ 中,$\angle BAC = 90^{\circ}$,$D$,$E$ 分别在线段 $AB$,$AC$ 上,$AD = AE$,$BE$ 和 $CD$ 交于点 $N$,$AF\perp BE$ 交 $BC$ 于点 $F$,$FG\perp CD$ 交 $AC$ 于点 $M$,交 $BE$ 的延长线于点 $G$.下列结论:①$\angle ABE = \angle FAC$;②$GE = ME$;③$BG = AF + FG$;④$C_{\triangle AFM} = BE + CM$;⑤$S_{\triangle BDN}:S_{\triangle AFC} = CE:AC$.其中正确的是

A.①③⑤
B.①②⑤
C.①②③
D.①③④

答案：
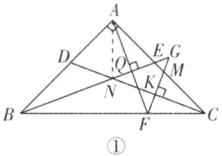
A 解析:设AF⊥BE于Q，FG⊥CD于K，如图①所示，
∵∠AQB = ∠BAC = 90°，
∴∠ABE + ∠BAQ = ∠FAC + ∠BAQ = 90°，
∴∠ABE = ∠FAC，故①正确；在△ABE与△ACD中，
$\begin{cases}AE = AD \\∠EAB = ∠DAC \\AB = AC\end{cases}$
∴△ABE≌△ACD(SAS)，
∴∠ABE = ∠ACD。
∵∠GEM = ∠AEB = 90° - ∠ABE，∠GME = ∠CMF = 90° - ∠ACD，
∴∠GEM = ∠GME，
∴GE = GM。若GM = EM，则△GEM为等边三角形，
∴∠AEB = ∠GEM = 60°，但题目中没有条件得到∠AEB = 60°，故②不一定成立；如图①所示，连接AN，由△ABE≌△ACD可得∠AEB = ∠ADC，
∴∠BDN = ∠CEN。
∵AD = AE，AB = AC，
∴BD = CE，在△BDN与△CEN中，
$\begin{cases}∠BND = ∠CNE \\∠BDN = ∠CEN \\BD = CE\end{cases}$
∴△BDN≌△CEN(AAS)，
∴BN = CN。又AB = AC，
∴AN垂直平分BC，
∴∠BAN = ∠EAN = 45°，
∴∠BAN = ∠ACF = 45°。在△ABN与△CAF中，
$\begin{cases}AB = CA \\∠ABN = ∠CAF \\∠BAN = ∠ACF\end{cases}$
∴△ABN≌△CAF(ASA)，
∴AN = CF，BN = AF。在△EAN与△MCF中，
$\begin{cases}∠AEN = ∠CMF \\∠EAN = ∠MCF \\AN = CF\end{cases}$
∴△EAN≌△MCF(AAS)，
∴NE = FM。又
∵GE = GM，
∴BG = BN + NE + GE = AF + FM + GM = AF + FG，故③正确；
∵BN = AF，NE = FM，
∴△AFM的周长为AF + FM + AM = BN + NE + AM = BE + AM。
∵△EAN≌△MCF，
∴AE = CM，
∴AM = AE + EM = CM + EM ＞ CM，
∴△AFM的周长 = BE + AM ＞ BE + CM，故④错误；如图②所示，过点N作NI⊥AB于I，过点F作FP⊥AC于P，
∵△ABN≌△CAF，
∴S△ABN = S△CAF，
∴$\frac{1}{2}$AB·NI = $\frac{1}{2}$AC·FP，
∴NI = FP，
∴$\frac{1}{2}$BD·NI = $\frac{1}{2}$CE·FP，即S△DBN = S△ECF。
∵S△CEF : S△AFC = CE : AC，
∴S△BDN : S△AFC = CE : AC，故⑤正确。故选A。

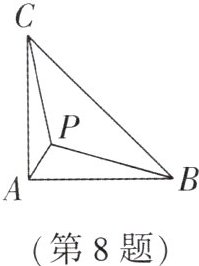
8. (长沙自主招生)如图,在等腰直角三角形 $ABC$ 中,$\angle BAC = 90^{\circ}$,$P$ 是 $\triangle ABC$ 内一点,$PA = 1$,$PB = 3$,$PC = \sqrt{7}$,那么 $\angle CPA = $______度.

答案：
135 解析:将△ABP绕点A逆时针旋转90°，然后连接PQ，则AQ = AP = 1，CQ = PB = 3，∠QAC = ∠PAB。
∵∠QAP = 90°，
∴∠QPA = 45°。又
∵∠PAB + ∠PAC = 90°，
∴∠PAQ = ∠QAC + ∠CAP = ∠PAB + ∠PAC = 90°，
∴PQ² = AQ² + AP² = 2，且∠QPA = 45°。在△CPQ中，PC² + PQ² = 7 + 2 = 9 = CQ²，
∴∠QPC = 90°，
∴∠CPA = ∠QPA + ∠QPC = 135°。故答案为135。

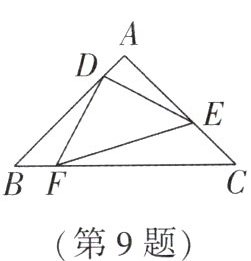
9. (南京自主招生)如图,$AB = AC = 3$,$\angle A = 90^{\circ}$,$AE = 2$,$\triangle DEF$ 为等腰直角三角形,则 $EF = $$\frac{\sqrt{34}}{2}$.

答案： $\frac{\sqrt{34}}{2}$ 解析:过点F作FH⊥AB于点H，
∴∠FHD = 90° = ∠A。
∵△ABC和△DEF均为等腰直角三角形，
∴∠FDE = ∠A = ∠FHD = 90°，DE = DF，∠B = 45°，EF = $\sqrt{2}$DF，
∴∠DFH + ∠HDF = 90° = ∠ADE + ∠HDF，
∴∠ADE = ∠DFH，
∴△ADE≌△HFD(AAS)，
∴HF = AD，AE = DH = 2。
∵∠B = 45°，HF⊥AB，
∴△BHF是等腰直角三角形，
∴BH = HF = AD。
∵AB = AC = 3，
∴BH + DH + AD = 3，
∴AD = HF = $\frac{1}{2}$，
∴DF = $\sqrt{DH² + HF²}$ = $\sqrt{4 + \frac{1}{4}}$ = $\frac{\sqrt{17}}{2}$，
∴EF = $\sqrt{2}$DF = $\frac{\sqrt{34}}{2}$。故答案为$\frac{\sqrt{34}}{2}$。

10. 如图,在等腰直角三角形 $ABC$ 中,$\angle BAC = 90^{\circ}$,$AB = AC = 2\sqrt{6}$,点 $M$ 是 $BC$ 边上一动点,将线段 $AM$ 绕点 $A$ 顺时针旋转 $60^{\circ}$,得到线段 $AN$,连接 $MN$,$CN$,则 $AN + CN$ 的最小值是______.

答案：
2$\sqrt{3}$ + 6 解析:如图，在BC上取一点D，使∠BAD = 60°，连接AD，在AB上截取AI = AD，连接DI，作直线IN。
∵∠BAC = 90°，AB = AC = 2$\sqrt{6}$，
∴∠CAD = 90° - ∠BAD = 30°，∠ACB = ∠ABC = 45°，BC = $\sqrt{AB² + AC²}$ = $\sqrt{2}$AC = $\sqrt{2}$×2$\sqrt{6}$ = 4$\sqrt{3}$，
∴∠ADM = ∠CAD + ∠ACB = 75°。
∵由旋转得AN = AM，∠MAN = 60°，
∴∠IAN = 60° - ∠BAM = ∠DAM。在△IAN和△DAM中，
$\begin{cases}AN = AM \\∠IAN = ∠DAM \\AI = AD\end{cases}$
∴△IAN≌△DAM(SAS)，
∴∠AIN = ∠ADM = 75°，
∴点N在经过AB上的定点I且与AB相交成的锐角等于75°的直线IN上运动，作点A关于直线IN的对称点F，连接AF交IN于点L，连接FN，FI，DI。
∵IN垂直平分AF，△ADI是等边三角形，
∴∠ALI = 90°，FN = AN，FI = AI = DI，∠AID = ∠ADI = 60°，
∴∠IFA = ∠IAF = 90° - ∠AIN = 15°，∠BID = 180° - ∠AID = 120°，
∴∠BIF = ∠IFA + ∠IAF = 30°，
∴∠DIF = ∠BID + ∠BIF = 150°，连接DF，则∠IDF = ∠IFD = $\frac{1}{2}$×(180° - ∠DIF) = 15°。
∵∠IDB = ∠ADM - ∠ADI = 15°，
∴∠IDF = ∠IDB，
∴点F在CB的延长线上，
∴∠AFD = ∠IFA + ∠IFD = 30°。作AE⊥BC于点E，则∠AEF = 90°，AE = CE = BE = $\frac{1}{2}$BC = 2$\sqrt{3}$，
∴AF = 2AE，
∴EF = $\sqrt{AF² - AE²}$ = $\sqrt{(2AE)² - AE²}$ = $\sqrt{3}$AE = $\sqrt{3}$×2$\sqrt{3}$ = 6，
∴CF = CE + EF = 2$\sqrt{3}$ + 6。
∵FN + CN ≥ CF，
∴AN + CN ≥ 2$\sqrt{3}$ + 6，
∴AN + CN的最小值是2$\sqrt{3}$ + 6。故答案为2$\sqrt{3}$ + 6。

11. 某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
(1)●操作发现
在等腰三角形 $ABC$ 中,$AB = AC$,分别以 $AB$ 和 $AC$ 为斜边,向 $\triangle ABC$ 的外侧作等腰直角三角形,如图①所示,其中 $DF\perp AB$ 于点 $F$,$EG\perp AC$ 于点 $G$,$M$ 是 $BC$ 的中点,连接 $MD$ 和 $ME$,则下列结论正确的是______.(填序号即可)
①$AF = AG = \frac{1}{2}AB$;②$MD = ME$;③整个图形是轴对称图形.
(2)●数学思考
在任意 $\triangle ABC$ 中,分别以 $AB$ 和 $AC$ 为斜边,向 $\triangle ABC$ 的外侧作等腰直角三角形,如图②所示,$M$ 是 $BC$ 的中点,连接 $MD$ 和 $ME$,则 $MD$ 和 $ME$ 具有怎样的数量和位置关系? 请给出证明过程.
(3)●类比探究
在任意 $\triangle ABC$ 中,仍分别以 $AB$ 和 $AC$ 为斜边,向 $\triangle ABC$ 的内侧作等腰直角三角形,如图③所示,$M$ 是 $BC$ 的中点,连接 $MD$ 和 $ME$,试判断 $\triangle MED$ 的形状.

答案：

(1)操作发现:①②③ 解析:
∵△ADB和△AEC是等腰直角三角形，
∴∠ABD = ∠DAB = ∠ACE = ∠EAC = 45°，∠ADB = ∠AEC = 90°。在△ADB和△AEC中，
$\begin{cases}∠ADB = ∠AEC \\∠ABD = ∠ACE \\AB = AC\end{cases}$
∴△ADB≌△AEC(AAS)，
∴BD = CE，AD = AE。
∵DF⊥AB于点F，EG⊥AC于点G，
∴AF = BF = DF = $\frac{1}{2}$AB，AG = GC = GE = $\frac{1}{2}$AC。
∵AB = AC，
∴AF = AG = $\frac{1}{2}$AB，故①正确；
∵M是BC的中点，
∴BM = CM。
∵AB = AC，
∴∠ABC = ∠ACB，
∴∠ABC + ∠ABD = ∠ACB + ∠ACE，即∠DBM = ∠ECM。在△DBM和△ECM中，
$\begin{cases}BD = CE \\∠DBM = ∠ECM \\BM = CM\end{cases}$
∴△DBM≌△ECM(SAS)，
∴MD = ME。故②正确；如图①，连接AM，根据前面的证明可以得出将图形①沿AM对折左右两部分能完全重合，
∴整个图形是轴对称图形，故③正确。故答案为①②③。
(2)数学思考:MD = ME，MD⊥ME。证明:如图②，延长EM至点N，使MN = EM，连接BN，DN，DE，
∵BM = CM，∠BMN = ∠CME，
∴△BMN≌△CME(SAS)，
∴BN = CE，∠NBM = ∠ECM。
∵△ABD和△AEC是等腰直角三角形，
∴∠DBA = ∠ECA = ∠DAB = ∠EAC = 45°，BD = DA，AE = EC = BN；
∴∠DBN = ∠DBM + ∠NBM = ∠DBM + ∠ECM = ∠DBA + ∠ABC + ∠ACB + ∠ECA = 90° + ∠ABC + ∠ACB = 90° + 180° - ∠BAC = 270° - ∠BAC，∠DAE = 360° - ∠DAB - ∠EAC - ∠BAC = 360° - 90° - ∠BAC = 270° - ∠BAC，
∴∠DBN = ∠DAE，
∴△DBN≌△DAE(SAS)，
∴∠BDN = ∠ADE，DN = DE，
∴∠NDE = ∠NDA + ∠ADE = ∠NDA + ∠NDB = ∠BDA = 90°，
∴△DNE是等腰直角三角形，
∴MD = ME，MD⊥ME。
(3)类比探究:如图③，延长EM至点N，使EM = MN，连接BN，DN，则BD = AD，EC = BN = AE，∠ECM = ∠NBM，
∴∠DAC = 45° - ∠EAD，∠ACB = 45° + ∠ECM，
∴∠DAC + ∠ACB = 90° - ∠EAD + ∠ECM。
∵∠DBC + ∠BDA = ∠DAC + ∠ACB，
∴∠DBC + 90° = 90° - ∠EAD + ∠ECM，
∴∠NBM - ∠NBD = ∠ECM - ∠EAD，
∴∠NBD = ∠EAD，
∴△NBD≌△EAD(SAS)，
∴∠BDN = ∠ADE，DN = ED，
∴∠NDE = 90°，
∴△MED为等腰直角三角形。