《2025年作业本江西教育出版社七年级数学上册北师大版》

1. 朱自清在《春》中写春雨“像牛毛，像花针，像细丝，密密地斜织着”，他把雨看成了线，这说明了点动成线。

答案： 点动成线

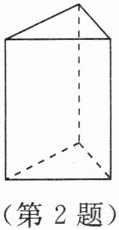
2. 如图所示，三棱柱底面边长都是3cm，侧棱长为5cm，此三棱柱共有3个侧面，所有棱长之和为33cm，侧面展开图的面积为45cm²。

答案： 3
33
45

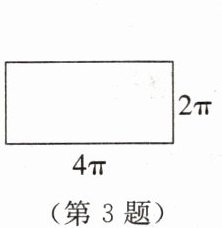
3. 如图所示，一个圆柱的侧面展开图是一个长方形，则这个圆柱的底面面积为4π 或 π(结果保留π)。

答案： 4π或π

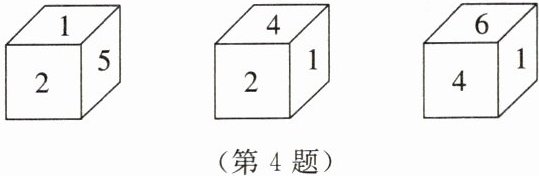
4. 正方体木块的六个面分别标有数字1，2，3，4，5，6，从不同方向观察这个正方体木块，看到的数字情况如图所示，则数字1和5对面的数字分别是3和4。

答案： 3
4

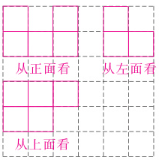
5. 由7个大小相同的小立方块搭成的几何体如图所示，请画出从正面、左面、上面看到的这个几何体的形状图。

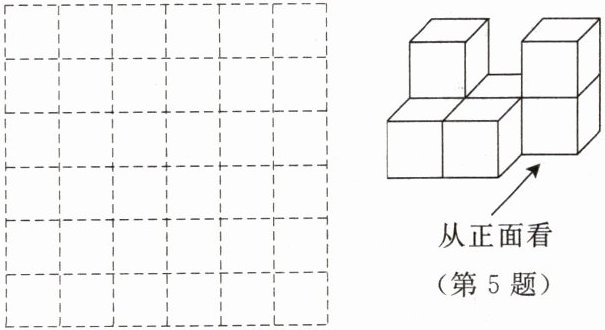
答案：

6. 小明在家用剪刀剪开了一个长方体纸盒，可是一不小心多剪了一条棱，把纸盒剪成了两部分，即下图中的①和②。根据你所学的知识，回答下列问题。
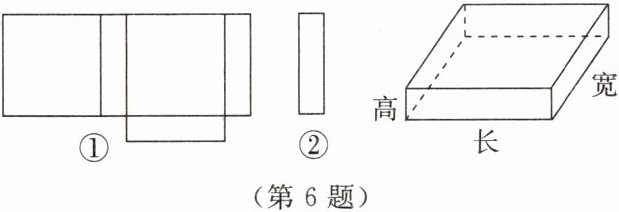
(1) 小明总共剪开了8条棱。
(2) 现在小明想将剪断的②重新粘贴回①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，你认为他应该将②粘贴到①中的什么位置上？请你帮助小明在①上补全(画出一种情况即可)。
(3) 小明说：“我剪的所有棱中，最短的一条棱长为2cm，最长的一条棱长是最短的那条棱长的5倍。”若纸盒的底面是一个正方形，求长方体纸盒的表面积和体积。

答案：
8
解：​
(2)​如图所示，有以下四种情况：

​
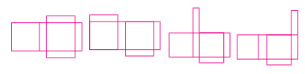
(3)​因为长方体纸盒的底面是一个正
方形，最短的棱长是高，为$​2\ \mathrm {cm}，$​
则长与宽相等，为$​10\ \mathrm {cm}。$​
表面积为
$​2×10×10 + 10×2×4 = 280(\mathrm {cm}^2)​$
体积为$​2×10×10 = 200(\mathrm {cm}^3)​$