《2025年作业本江西教育出版社七年级数学上册北师大版》

1. 用计算器计算$(-3)^{3}×6$，按键顺序为。

答案：

2. 如图所示，按下面的程序进行运算。

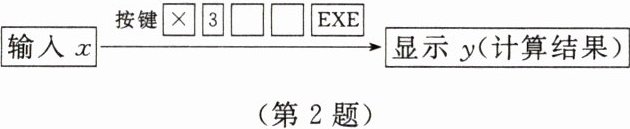
下表中的$x$与$y$分别是输入的$6$个数及相应的计算结果：

当在计算器上输入的$x$值为$-10$时，计算器输出的$y$值为-29。

答案： -29

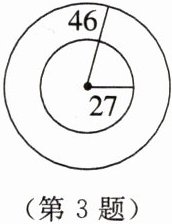
3. 如图所示，已知圆环的外圆半径为$46\mathrm{mm}$，内圆半径为$27\mathrm{mm}$，利用计算器求圆环的面积（$\pi$取$3.14$）。

答案： 解：$​3.14×46^2 - 3.14×27^2​$
$​= 4355.18(\text{mm}^2)​$

4. 用计算器进行探索：任写一个数，它是$3$的倍数，把它各个数位上的数字分别立方，再把得到的立方数相加，得到一个新的数。将上述新得到的数的各个数位上的数字分别立方，再将由此得到的立方数相加，又得到一个新数，一直重复下去。你发现了什么？

答案： 解：最后结果永远是153。

5. 用计算器求下列各式的值。
(1)$24.1^{2}×2 + 3.45^{2}×4.2$（结果精确到$0.1$）；
(2)$(2.4^{2}-1.3^{2})×3.1 + 4.1^{3}$（结果精确到$0.01$）。

答案： 解：原式≈1211.6。
解：原式≈81.54。

6. 为了比较$2024^{2025}$和$2025^{2024}$的大小，我们可以从简单的情况入手，从中发现规律，经过归纳猜想得出结论。
(1) 比较大小：
①$1^{2}$＜$2^{1}$；②$2^{3}$＜$3^{2}$；③$3^{4}$＞$4^{3}$；④$4^{5}$＞$5^{4}$；⑤$5^{6}$＞$6^{5}$。
(2) 猜想$n^{n + 1}$与$(n + 1)^{n}$($n$为正整数)的大小关系。
(3) 根据(2)中的结论，比较大小：$2024^{2025}$＞$2025^{2024}$。

答案： ＜
＜
＞
＞
＞
＞
解：​
(2)​当​n ＜ 3​时，$​n^{n + 1} ＜ (n + 1)^n；$​
当$​n\geq 3​$时，$​n^{n + 1} ＞ (n + 1)^n。$​