《2025年作业本江西教育出版社七年级数学上册北师大版》

1. 下面这一列数 $2,-4,6,-8,10,\cdots$，第 $2025$ 个数是4050。

答案： 4050

2. 蟋蟀鸣叫的次数与气温存在一定的关系。某学习小组记录了当地不同气温下某种蟋蟀每分钟鸣叫的次数，如下表所示：

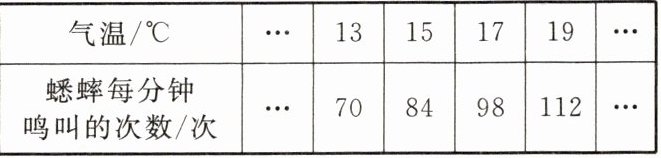
若测得这种蟋蟀每分钟鸣叫 $49$ 次，则该地当时的气温约为10℃。

答案： 10℃

3. 刘老师接到一个紧急通知，需要尽快用电话通知全班 $45$ 名同学。如果每通知一名同学需要 $1\min$，且接到通知的同学可以立即帮助通知其他人，那么要使所有同学都接到通知，最快需要6$\min$。

答案： 6

4. 生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型。在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型 $2^{n}$ 来表示，即 $2^{1}=2$，$2^{2}=4$，$2^{3}=8$，$2^{4}=16$，$2^{5}=32$，$\cdots$。请你推算 $2^{1}+2^{2}+2^{3}+2^{4}+2^{5}+\cdots+2^{2025}$ 的个位数字是2。

答案： 2

5. $2024$ 年是龙年，$2049$ 年是蛇年。

答案： 蛇

6. 在图①和图②的空格中填入不大于 $15$ 且互不相同的数，使每一横行、每一竖列和对角线上的三个数之和都等于 $30$。

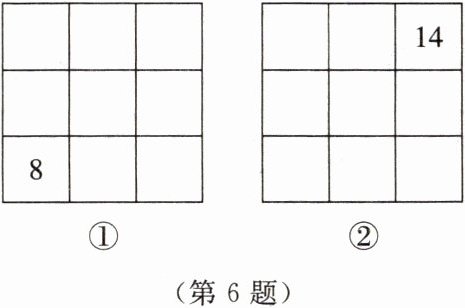
答案：

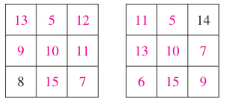
7. 如图所示，将一串有理数按下列规律排列，回答下列问题。
（1）在 $B$ 处的数是正数还是负数？
（2）在 $A,B,C,D$ 中哪个位置的数是正数？
（3）第 $2023$ 个数是正数还是负数？排在 $A,B,C,D,E$ 中的哪个位置？

答案： 解：
(1)负数。
(2)A，C位置的数是正数。
(3)第2023个数是负数，排在D的位置。