《2025年作业本江西教育出版社七年级数学上册北师大版》

1. 如图所示，某幼儿园举行用火柴棒摆“金鱼”比赛，请观察图形排列规律，并解答下列问题：按照此规律，摆第 10 个图时，需62根火柴棒；摆第$n$个图时，需(6n+2)根火柴棒。

答案： 62
6n+2

2. 下图是按照一定规律画出的“树形图”，经观察可以发现：图①有 1 个“树枝”，图②有 3 个“树枝”，图③有 7 个“树枝”……照此规律，图⑥有63个“树枝”。

答案： 63

3. “幻方”最早记载于春秋时期的《大戴礼》中，现将 1，2，3，4，5，7，8，9 这八个数字填入如图①所示的“幻方”中，使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等。现有如图②所示的“幻方”，则$(x - y)^{m - n}$的值是-27。

答案： -27

4. 将一张纸对折 1 次可以得到 2 层，对折 2 次可以得到 4 层，照这样一直折下去。
(1) 对折 6 次可以得到64层。
(2) 如果一张纸的厚度是$0.1\mathrm{mm}$，求对折 6 次后纸的总厚度。

答案： 64
解：对折​6​次时，纸的层数为$​2^6 = 64，$
$​​0.1 ×64 = 6.4(\text{mm})。$​
故对折​6​次后纸的总厚度为$​6.4 \text{mm}。$​

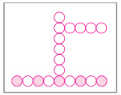
5. 下图是用棋子摆成的“上”字图案。
(1) 根据上面的规律，请在方框中画出第 4 个图案。
(2) 按照这样的规律摆下去，摆成第$n$个“上”字图案需要黑子(n+1)个，白子(3n+2)个。(用含$n$的代数式表示)
(3) 第8个“上”字图案的白子数量比黑子数量多 17 个。

答案：

n+1
3n+2
8