第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 下列说法正确的是(
A.画直线 $ AB = 10\ cm $
B.已知 $ A $,$ B $,$ C $ 三点,过这三点画一条直线
C.延长射线 $ OB $
D.取线段 $ AB $ 的中点 $ C $
D
)A.画直线 $ AB = 10\ cm $
B.已知 $ A $,$ B $,$ C $ 三点,过这三点画一条直线
C.延长射线 $ OB $
D.取线段 $ AB $ 的中点 $ C $
答案:
D
2. 如图所示,在长方形纸片 $ ABCD $ 中,点 $ E $,$ F $ 分别在边 $ AB $,$ CD $ 上,连接 $ EF $。将 $ \angle BEF $ 对折,点 $ B $ 落在直线 $ EF $ 上的点 $ B' $ 处,得折痕 $ EM $;将 $ \angle AEF $ 对折,点 $ A $ 落在直线 $ EF $ 上的点 $ A' $ 处,得折痕 $ EN $。$ \angle NEM $ 的大小为(
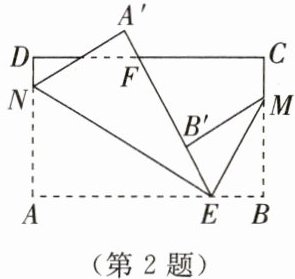
A.$ 105^{\circ} $
B.$ 90^{\circ} $
C.$ 60^{\circ} $
D.不能确定
B
)
A.$ 105^{\circ} $
B.$ 90^{\circ} $
C.$ 60^{\circ} $
D.不能确定
答案:
B
3. 经过多边形的一个顶点的所有对角线把多边形分成 $ 9 $ 个三角形,这个多边形经过这一顶点的对角线的条数是
8
。
答案:
8
4. 将一个圆分割成三个扇形,它们的圆心角的度数比为 $ 1:1:2 $,那么这三个扇形的圆心角的度数分别是________________。
答案:
90°,90°,
180°
180°
5. 先作图,再解答:在直线 $ l $ 上顺次取 $ A $,$ B $,$ C $ 三点,使 $ AB = 2\ cm $,$ BC = 3\ cm $,$ O $ 是线段 $ AC $ 的中点。求线段 $ OB $ 的长。
答案:
解:
 因为$AB=2\ \mathrm {cm},$$BC=3\ \mathrm {cm},$
因为$AB=2\ \mathrm {cm},$$BC=3\ \mathrm {cm},$
所以$AC=AB+BC=2+3=5(\mathrm {cm})。$
又因为O是线段AC的中点,
所以$AO=OC=\frac {1}{2}AC=\frac {1}{2}×5=\frac {5}{2}(\mathrm {cm}),$
所以$OB=AO-AB=\frac {5}{2}-2=\frac {1}{2}(\mathrm {cm})。$
解:
 因为$AB=2\ \mathrm {cm},$$BC=3\ \mathrm {cm},$
因为$AB=2\ \mathrm {cm},$$BC=3\ \mathrm {cm},$ 所以$AC=AB+BC=2+3=5(\mathrm {cm})。$
又因为O是线段AC的中点,
所以$AO=OC=\frac {1}{2}AC=\frac {1}{2}×5=\frac {5}{2}(\mathrm {cm}),$
所以$OB=AO-AB=\frac {5}{2}-2=\frac {1}{2}(\mathrm {cm})。$
6. 如图所示,已知点 $ C $ 在线段 $ AB $ 上,且 $ AC = 6 $,$ BC = 14 $,$ M $,$ N $ 分别是 $ AC $,$ BC $ 的中点。
(1) 求线段 $ MN $ 的长。
(2) 如果 $ AC = a $,$ BC = b $,其他条件不变,你能猜测出 $ MN $ 的长度吗?请写出你的结论,并说明理由。

(1) 求线段 $ MN $ 的长。
(2) 如果 $ AC = a $,$ BC = b $,其他条件不变,你能猜测出 $ MN $ 的长度吗?请写出你的结论,并说明理由。

答案:
解:
(1)因为AC=6,BC=14,M,
N分别是AC,BC的中点,
所以MC=3,NC=7,
所以MN=MC+NC=10。
$ (2)MN=\frac {1}{2}(a+b)。$
理由如下:
因为AC=a,BC=b,M,N分别
是AC,BC的中点,
所以$MC=\frac {1}{2}a,$$NC=\frac {1}{2}b,$
所以$MN=MC+NC=\frac {1}{2}(a+b)。$
(1)因为AC=6,BC=14,M,
N分别是AC,BC的中点,
所以MC=3,NC=7,
所以MN=MC+NC=10。
$ (2)MN=\frac {1}{2}(a+b)。$
理由如下:
因为AC=a,BC=b,M,N分别
是AC,BC的中点,
所以$MC=\frac {1}{2}a,$$NC=\frac {1}{2}b,$
所以$MN=MC+NC=\frac {1}{2}(a+b)。$
查看更多完整答案,请扫码查看


