《2025年作业本江西教育出版社七年级数学上册北师大版》

8. 用小立方块搭一个几何体，使其从正面和从上面看到的形状图如图所示。其中，从上面看到的形状图中，每个小正方形中的字母表示该位置小立方块的个数，请解答下列问题。
(1) $a =$3，$b =$1，$c =$1。
(2) 这个几何体最少由9个小立方块搭成，最多由11个小立方块搭成。
(3) 当 $d = e = 1$，$f = 2$ 时，画出从左面看到的几何体的形状图。

答案：
3
1
1
9
11
解：
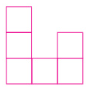
(3)从左面看到的形状图有3列，每列小正方形的数目分别为3，1，2，所以从左面看到的几何体的形状图如图所示。

9. 如图所示，图①为一个棱长为8的正方体，图②为图①的表面展开图(数字和字母写在外表面上，字母也可以表示数)，请根据要求解答下列问题。
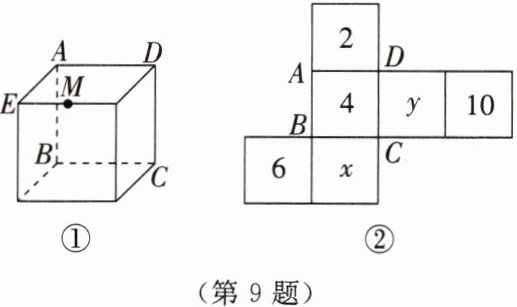
(1) 若正方体相对面上的两个数字之和相等，则 $x =$12，$y =$8。
(2) 若数字“10”在左面，数字“6”在前面，则在上面的是2(填“$x$”“$y$”或“2”)。
(3) 图①中，$M$ 为所在棱的中点，在图②中找出点 $M$ 的位置，并求出图②中三角形 $ABM$ 的面积。

答案：
12
8
2
解：​
(3)​因为点​M​所在的棱为两个面共用，
所以它的位置有两种情况。
第一种情况如下图所示：

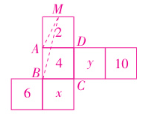
$​S_{三角形ABM}=\frac {1}{2}×8×\frac {1}{2}×8 = 16。$​
第二种情况如下图所示：

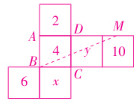
$​S_{三角形ABM}=\frac {1}{2}×8×(8 + 8+\frac {1}{2}×8)=80。$​
综上所述，三角形​ABM​的面积为​16​或​80。​