第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 手电筒发出的光束、舞台上的光束、投影仪的光束$\cdots\cdots$都可以近似地看作
射
线。
答案:
射
2. 如图所示,下列说法不正确的是____(填序号)。
①直线$AC$与直线$AD$是不同的直线;②射线$AB$与射线$BA$是同一条射线;③线段$AB$与线段$BA$是同一条线段;④直线$AD=AB+BC+CD$。
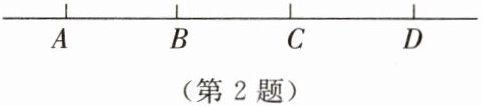
①直线$AC$与直线$AD$是不同的直线;②射线$AB$与射线$BA$是同一条射线;③线段$AB$与线段$BA$是同一条线段;④直线$AD=AB+BC+CD$。

答案:
①②
④
④
3. 射击运动员在射击时,通过枪上的准星去瞄准目标,此时眼睛和准星确定了一条直线,这条直线指向目标,从而提高了射击的准确性。这种方法所运用的数学原理是
两点确定一条直线
。
答案:
两点确定一条直线
4. 如图所示,棋盘上有黑、白两色棋子若干枚,如果在一条至少有两枚棋子的直线(包括图中没有画出的直线)上只有颜色相同的棋子,我们就称为“同棋共线”。图中“同棋共线”的线共有

10
条。
答案:
10
5. (1)如图①所示,有不在同一直线上的三点,每两点连一条线段,可以连几条线段?
(2)如图②所示,有四个点,且任意三点都不在同一直线上,每两点连一条线段,可以连几条线段?

(2)如图②所示,有四个点,且任意三点都不在同一直线上,每两点连一条线段,可以连几条线段?

答案:
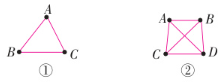
解:
(1)可以连3条线段。
(2)可以连6条线段。
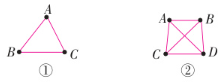
解:
(1)可以连3条线段。
(2)可以连6条线段。
6. (1)如图所示,线段$AB$上有$C$,$D$两个点,请计算图中共有多少条线段。
(2)如果线段上有$m$个点(包括线段的两个端点),那么该线段上共有多少条线段?
(3)如果$8$个班参加学校组织的篮球比赛,比赛采用单循环制(即每两个班级之间都要进行一场比赛),那么一共要进行多少场比赛?

(2)如果线段上有$m$个点(包括线段的两个端点),那么该线段上共有多少条线段?
(3)如果$8$个班参加学校组织的篮球比赛,比赛采用单循环制(即每两个班级之间都要进行一场比赛),那么一共要进行多少场比赛?

答案:
解:
(1)6条。
(2)m - 1 + m - 2 + m - 3 + m - 4 +
$…+ 2 + 1=\frac {m(m - 1)}{2}($条)
(3)8×(8 - 1)÷2 = 28(场)
(1)6条。
(2)m - 1 + m - 2 + m - 3 + m - 4 +
$…+ 2 + 1=\frac {m(m - 1)}{2}($条)
(3)8×(8 - 1)÷2 = 28(场)
查看更多完整答案,请扫码查看


