《2025年作业本江西教育出版社七年级数学上册北师大版》

11. 若$5a^{4}b$与$2a^{2x}b^{y}$是同类项，则$x^{2} - y =$3。

答案： 3

12. 若有理数$a$，$b$满足$|a| = 3$，$b^{2} = 16$，且$|a + b| = -(a + b)$，则$a - 2b$的值为5或11。

答案： 5或11

13. 计算。
（1）$-4\dfrac{1}{3} - 5\dfrac{1}{2} + 7\dfrac{1}{3}$；
（2）$-1^{2} + (-5) × \left(-\dfrac{8}{5}\right) - (-4)^{2} ÷ (-8)$。

答案： 解：原式$​=7\frac {1}{3}-4\frac {1}{3}-5\frac {1}{2}​$
$​                =3-5\frac {1}{2}​$
$​                =-2\frac {1}{2}​$
解：原式​=-1+8-(-2)​
​                =7+2​
​                =9​

14. 画出数轴，在数轴上表示下列各数，并用“$＜$”将它们连接起来。
$-\left(-\dfrac{5}{2}\right)$，$-3.5$，$0$，$|-3|$，$-2^{2}$，$-1\dfrac{1}{2}$。

答案：
解：数轴及点的表示如图所示。

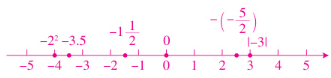
$​-2²＜-3.5＜-1\frac {1}{2}＜0＜-(-\frac {5}{2})＜$|-3|​

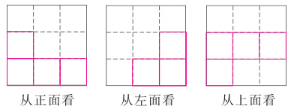
15. 如图所示，一个几何体由$5$个大小相同的小立方块搭成，请分别画出从正面、左面、上面看到的这个几何体的形状图。

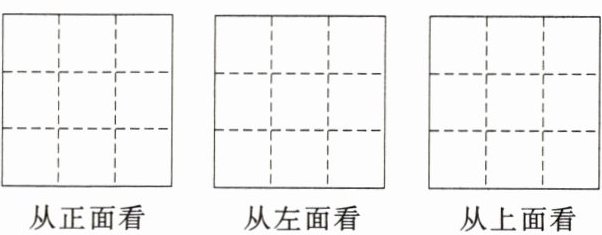
答案：

16. 先化简，再求值：$5x + 13(x^{2} - y) - 5\left(3x^{2} + x - \dfrac{1}{5}y\right) + 10y$，其中$x = -3$，$y = 2$。

答案： 解：原式=5x+13x²-13y-15x²-5x+y+10y
=-2x²-2y。
当x=-3，y=2时，
原式=-2×(-3)²-2×2=-2×9-4=-18-4=-22

17. 若$a$，$b$互为相反数，$c$，$d$互为倒数，$|m| = 3$，求$\dfrac{a + b}{4m} + m^{2} - 3cd + 5m$的值。

答案： 解：依题意，得
​a+b=0，​​cd=1，​​m=±3。​
当​m=3​时，
原式​=0+3²-3×1+5×3​
​=9-3+15=21；​
当​m=-3​时，
原式​=0+(-3)²-3×1+5×(-3)​
​=9-3-15=-9。​
因此$​\frac {a+b}{4m}+m²-3cd+5m ​$的值为
​21​或​-9。​