《2025年作业本江西教育出版社七年级数学上册北师大版》

1. 若一个数是 11，另一个数比 11 的相反数大 2，则这两个数的和是2。

答案： 2

2. 若 $ a $ 是最小的正整数，$ b $ 是最大的负整数，$ c $ 是绝对值最小的有理数，则 $ a + b + c = $0。

答案： 0

3. 绝对值大于 3 且不大于 7 的所有整数的和为0。

答案： 0

4. 计算：$ 1 + (-2) + 3 + (-4) + 5 + (-6) + 7 + (-8) + \cdots + 2025 = $1013。

答案： 1013

5. 计算。
(1) $ (-1.9) + 3.6 + (-10.1) + 1.4 $；
(2) $ (-7) + 11 + (-13) + 9 $；
(3) $ (-2.6) + (-3.4) + 2.3 + 1.5 - 2.3 $；
(4) $ (-26.5) + (-6.4) + (-18.5) + 6.4 $。

答案： 解：原式=-1.9+3.6-10.1+1.4
= -7
解：原式=-7+11-13+9
                =0
解：原式=-2.6-3.4+2.3+1.5-2.3
                =-4.5
解：原式=-26.5-6.4-18.5+6.4
                =-45

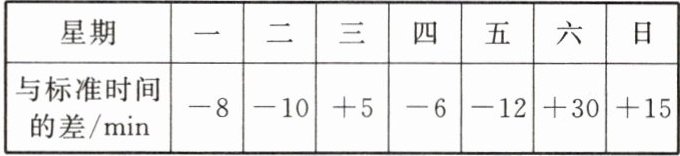
6. 为落实“双减”政策要求，学校对课后作业时长进行了科学调控。小明记录了本星期写课后作业的时间，数据如下表所示(以 60 min 为标准，时间多于 60 min 用正数表示，时间少于 60 min 用负数表示)：
(1) 这一星期内写课后作业用时最多的是星期六，用时最少的是星期五。
(2) 求小明这一星期每天写课后作业的平均时间。

答案： 六
五
解：
(2)60+(-8-10+5-6-12+30+15)÷7=62(min)
答：小明这一星期每天写课后作业的
平均时间为62min。

7. 阅读下面的材料。
对于 $ \left( -5\frac{5}{6} \right) + \left( -9\frac{2}{3} \right) + 17\frac{3}{4} + \left( -3\frac{1}{2} \right) $，可以按如下方法计算：
解：原式 $ = (-5) + \left( -\frac{5}{6} \right) + (-9) + \left( -\frac{2}{3} \right) + 17 + \frac{3}{4} + (-3) + \left( -\frac{1}{2} \right) $
$ = [(-5) + (-9) + 17 + (-3)] + \left[ \left( -\frac{5}{6} \right) + \left( -\frac{2}{3} \right) + \frac{3}{4} + \left( -\frac{1}{2} \right) \right] $
$ = 0 + \left( -1\frac{1}{4} \right) $
$ = -1\frac{1}{4} $。
上面这种方法叫作拆项法。仿照上述方法，计算：$ \left( -2018\frac{5}{6} \right) + \left( -2017\frac{2}{3} \right) + \left( -1\frac{1}{2} \right) + 4036 $。

答案： 解：原式$​=(-2018)+(-\frac {5}{6})+(-2017)+​$
$​                     (-\frac {2}{3})+(-1)+(-\frac {1}{2})+4036​$
​                 =[(-2018)+(-2017)+(-1)+​
$​                  4036]+[(-\frac {5}{6})+(-\frac {2}{3})+(-\frac {1}{2})]​$
​                =0+(-2)​
​                =-2​