《2025年作业本江西教育出版社七年级数学上册北师大版》

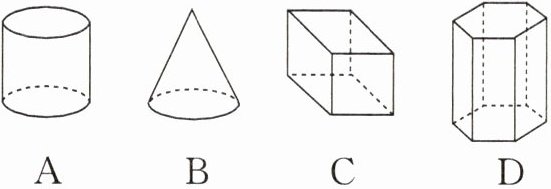
1. 下列几何体中，由3个面围成的是(A)

答案： A

2. 中华武术是我国传统文化的瑰宝。谚语“枪挑一条线，棍扫一大片”从数学的角度解释为点动成线，线动成面。

答案： 点动成线，线动成面

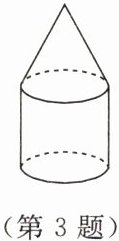
3. 如图所示，该几何体可以近似地看成是由圆锥和圆柱组合而成的。

答案： 圆柱
圆锥

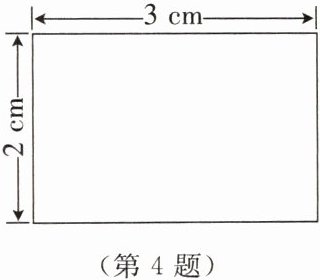
4. 一张长方形纸片的长和宽分别为3cm和2cm，如图所示。将该纸片绕其一条边所在的直线旋转一周。
(1)旋转形成的几何体是圆柱。
(2)这一现象说明的几何原理是(C)
A. 点动成线 B. 线动成面 C. 面动成体
(3)求旋转一周形成的几何体的体积(结果保留π)。

答案： 圆柱
C
解：​
(3)​绕长所在的直线旋转一周得到
的圆柱体的体积为$​π×2^2×3 = 12π(\mathrm {cm}^3)。$​
绕宽所在的直线旋转一周得到的圆柱
体的体积为$​π×3^2×2 = 18π(\mathrm {cm}^3)。$​

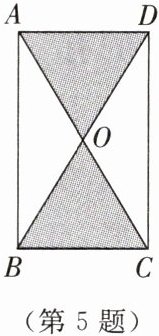
5. 如图所示，四边形ABCD是长方形，BC=6cm，AB=10cm，长方形的对角线AC和BD相交于点O。若将图中的阴影部分绕CD所在直线旋转一周，则阴影部分扫过的立体图形的体积是多少立方厘米（结果保留π）？

答案： 解：设三角形​BOC​以​CD​所在直线为轴
旋转一周所得到的立体图形的体积是
​V，​则
$​V=\frac {1}{3}×\pi ×6^2×10 - 2×\frac {1}{3}×\pi ×3^2×5​$
$​=120\pi - 30\pi = 90\pi (\mathrm {cm}^3)​$
所以$​2V = 180\pi\mathrm {cm}^3。$​
答：阴影部分扫过的立体图形的体积
是$​180\pi\mathrm {cm}^3。$​