《2025年作业本江西教育出版社七年级数学上册北师大版》

1. 在数轴上，表示+2的点在原点的右侧，距原点2个单位长度；表示-7的点在原点的左侧，距原点7个单位长度。

答案： 右
2
左
7

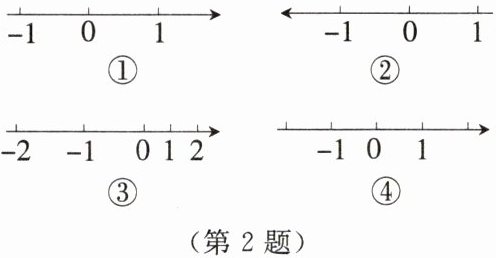
2. 下图中，表示数轴的是①④(填序号)。

答案： ①④

3. 画出数轴，在数轴上表示出下列各数：-1.5，-2，0，|-1|，3，并用“＜”将这些数连接起来。

答案：
解：
​-2 ＜ -1.5 ＜ 0 ＜ |-1| ＜ 3​

4. 某景区的部分景点和游览路线恰好都在一条直线上，一辆景区电瓶车接到任务从景区大门出发，向东走2km到达A景点，继续向东走2.5km到达B景点，然后又掉头向西走8.5km到达C景点，最后回到景区大门。
（1）以景区大门为原点，向东为正方向，以1个单位长度表示1km，建立如图所示的数轴，请在数轴上表示出上述三个景点的位置，并直接写出A，C两个景点间的距离。
（2）若该景区电瓶车充满一次电能行驶15km，则该景区电瓶车能否在一开始充满电而途中不充电的情况下完成此次任务？

答案：

解：
(1)A，B，C在数轴上的位置如图所示。A，C两个景点间的距离是6km。
(2)该景区电瓶车一共走的路程为17km，所以不能完成此次任务。

5. 一般地，数轴上表示数m和数n的两点之间的距离等于|m-n|。结合数轴与绝对值的知识，解答下列问题。
(1)数轴上表示5和1的两点之间的距离是4，表示-3和2的两点之间的距离是5。
（2）若数轴上表示数a的点与表示-2的点之间的距离是2，则a=。
(3)若数轴上表示数a的点在表示-4和2的两点之间，则|a + 4| + |a - 2|=6。
(4)所有满足|x + 2| + |x - 5|=7的整数x的和是12。
(5)当a=1时，|a + 5| + |a - 1| + |a - 3|的值最小，最小值是8。
(6)若x表示一个有理数，则|x - 1| + |x - 2| + |x - 3| + |x - 4| + ... + |x - 99| + |x - 100|的最小值是2500。

答案： 4
5
0或
-4
6
12
1
8
2500