《2025年作业本江西教育出版社七年级数学上册北师大版》

18. 我们规定一种新运算“$\#$”：对于任意有理数$a$，$b$，有$a\#b = a - b - 1$。例如：$-1\#1 = -1 - 1 - 1 = -3$。
（1）求$1\#2$和$1\#(-2)$的值。
（2）试猜想此种新运算是否满足交换律，说说你的理由。

答案： 解：​
(1) 1\#2 = 1 - 2 - 1 = -2。​
​1\#(-2) = 1 - (-2) - 1 = 2。​
​
(2) ​此种新运算不满足交换律。
理由如下：
因为​ a\#b = a - b - 1，
​​b\#a = b - a - 1，
$​​a - b - 1 \neq b - a - 1，$​
故不满足交换律。

19. 一名足球守门员练习折返跑，从球门的位置出发，向前记作正数，返回记作负数，他的记录如下（单位：$m$）：$+5$，$-3$，$+10$，$-8$，$-6$，$+12$，$-10$。
（1）该守门员是否回到了原来的位置？
（2）该守门员距离球门最远是多少米？
（3）该守门员一共跑了多少米？

答案： 解：
(1)根据题意，得
5-3+10-8-6+12-10=0(m)，
故该守门员回到了原来的位置。
(2)该守门员离开球门的位置分别距离球门5m，2m，12m，4m，2m，10m，0m，所以他距离球门最远是12m。
(3)总路程=|+5|+|-3|+|+10|+|-8|+|-6|+
|+12|+|-10|=54(m)。
故该守门员一共跑了54m。

20. 已知代数式$A = 3x^{2}y^{2} + xy - 1$，代数式$B = -x^{2}y^{2} - y + 1$，代数式$C = 2A - (A - 3B)$。
（1）化简代数式$C$。
（2）若代数式$C$的值与$y$的取值无关，求$x$的值。

答案： 解：
(1)由题意，得
C=2A-(A-3B)
=A+3B
=(3x²y²+xy-1)+3(-x²y²-y+1)
=xy-3y+2。
(2)因为C=y(x-3)+2，且代数式C的值与y的取值无关，
所以x-3=0，得x=3

21. 已知$A$，$B$两点在数轴上分别表示$a$，$b$。
（1）对照数轴填写下表：

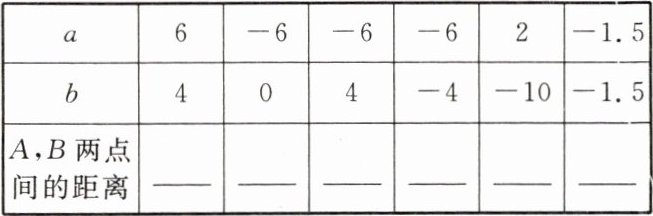
（2）若$A$，$B$两点间的距离记为$d$，试求$d$和$a$，$b$之间的数量关系。
（3）在数轴上标出所有符合条件的整数点$P$，使它到表示$10$的点和表示$-10$的点的距离之和为$20$，并求出这些整数的和。

答案：
2
6
10
2
12
0
解：
(2)d=|a-b|。
(3)整数点P可以为±10，±9，±8，±7，±6，±5，±4，±3，±2，±1，0，

因此，这些整数的和为0。