《2025年作业本江西教育出版社七年级数学上册北师大版》

6. 如图所示，将一个三阶魔方的表面进行涂色。观察发现，有的小正方体有一个面被涂色，有的小正方体有两个面被涂色，有的小正方体有三个面被涂色，有的小正方体所有面都没有被涂色。
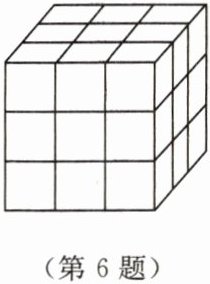
(1) 在三阶魔方中，所有面均未被涂色的小正方体有1个，只有一个面被涂色的小正方体有6个，有两个面被涂色的小正方体有12个，有三个面被涂色的小正方体有8个。
(2) 若为四阶魔方，则所有面均未被涂色的小正方体有8个，有三个面被涂色的小正方体有8个。
(3) 对于$n$阶魔方，所有面均未被涂色的小正方体有(n-2)^{3}个。
(4) 如果所有面均未被涂色的小正方体有 216 个，那么应该是八阶魔方。

答案： 1
6
12
8
8
8
$(n-2)^3$
八

7. 观察与思考：我们知道$1 + 2 + 3 + \cdots + n=\frac{n(n + 1)}{2}$，那么$1^{3} + 2^{3} + 3^{3} + \cdots + n^{3}$的结果等于多少呢？
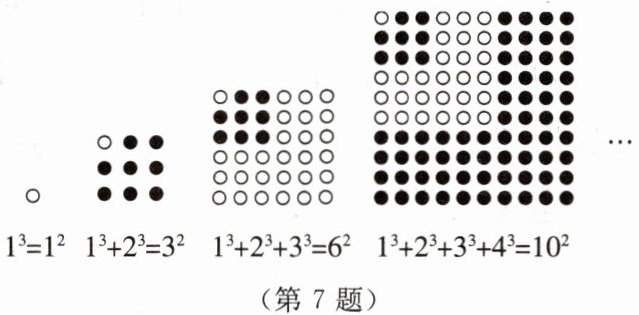
请你仔细观察，找出下面图形与算式的关系，解决下列问题。
(1) 尝试：第 5 个图形可以表示的等式是1^{3}+2^{3}+3^{3}+4^{3}+5^{3}=15^{2}。
(2) 概括：$1^{3} + 2^{3} + 3^{3} + \cdots + n^{3}=$\frac{n^{2}(n+1)^{2}}{4}$$。
(3) 应用：求$\frac{1^{3} + 2^{3} + 3^{3} + \cdots + 2024^{3}}{1 + 2 + 3 + \cdots + 2024}$的值。

答案： $1^3 + 2^3 + 3^3 + 4^3 + 5^3 = 15^2$
$\frac{n^2(n+1)^2}{4}$
解：$​(3)\frac {1^3 + 2^3 + 3^3 + … + 2024^3}{1 + 2 + 3 + … + 2024}​$
$​ =\frac {\frac {2024^2 ×2025^2}{4}}{\frac {2024 ×2025}{2}}​$
$​ =\frac {2024 ×2025}{2}​$
​ =2049300​