《2025年作业本江西教育出版社七年级数学上册北师大版》

1. 如图所示，某舰艇行驶到 $ B $ 处时，测得海岛 $ A $、轮船 $ C $ 的方向分别为北偏西 $ 30^{\circ} $ 和西南方向，则 $ \angle ABC $ 的大小是105°。

答案： 105°

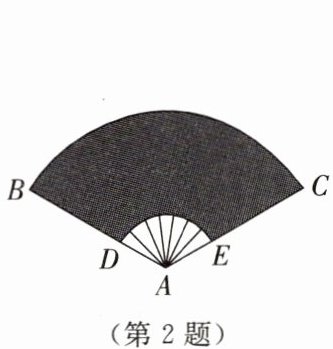
2. 如图所示，扇形纸折扇完全打开后，扇形 $ BAC $ 的面积为 $ 300\pi \, cm^2 $，$ \angle BAC = 120^{\circ} $，$ BD = 2AD $，则 $ BD $ 的长度为20 $ cm $。

答案： 20

3. 如图所示，已知射线 $ OC $，作 $ \angle AOB $，使它的平分线为射线 $ OC $。（尺规作图，不写作法，保留作图痕迹，并标出所作的角）

答案：

4. 如图所示，点 $ C $，$ D $，$ E $ 将线段 $ AB $ 分成四个部分，且 $ AC : CD : DE : EB = 2 : 3 : 4 : 5 $，$ M $，$ P $，$ Q $，$ N $ 分别是 $ AC $，$ CD $，$ DE $，$ EB $ 的中点，且 $ MN = 21 $，求 $ PQ $ 的长。

答案： 解：因为​ AC：CD：DE：EB = 2：3：​
​4：5 = 4：6：8：10，​
所以​ MC：CD：DE：EN = 2：6：8：5。​
因为​ MN = 21，​所以​ CD = 6，​​DE = 8，​
所以$​ PQ=\frac {1}{2}CD+\frac {1}{2}DE=\frac {1}{2}(6 + 8)=7。$​

5. （1）如图①所示，将一副三角尺的直角顶点重合在点 $ O $ 处。$ \angle AOD $ 和 $ \angle BOC $ 相等吗？请说明理由。$ \angle AOC $ 和 $ \angle BOD $ 有怎样的数量关系？请说明理由。
（2）若将这副三角尺按图②所示摆放，三角尺的直角顶点重合在点 $ O $ 处。$ \angle AOD $ 和 $ \angle BOC $ 相等吗？请说明理由。（1）中 $ \angle AOC $ 和 $ \angle BOD $ 的数量关系还成立吗？请说明理由。

答案： 解：
(1) 因为 ​​∠AOD = ∠AOB + ∠BOD​​，
​​∠BOC = ∠BOD + ∠COD​​，
且∠AOB = ∠COD = 90°​​，
所以 ​​∠AOD = ∠BOC​​。
因为 ​​∠AOC + 90° + ∠BOD + 90° = 360°​​，
所以 ​​∠AOC + ∠BOD = 180°​​。
(2) ​​∠AOD = ∠BOC​​。
因为 ​​∠AOD + ∠DOB = 90°​​，​​
∠BOC + ∠BOD = 90°​​，
所以 ​​∠AOD = ∠BOC​​。
成立。由 ​​∠AOC = 90° + 90° - ∠BOD​​ 
可知，​​∠AOC + ∠BOD = 180°​​。